
2、已知命题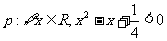 ;命题
;命题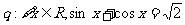 ,则下列判断正确的是 (
▲ )
,则下列判断正确的是 (
▲ )
A. 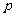 是真命题 B.
是真命题 B. 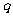 是假命题 C.
是假命题 C. 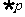 是假命题 D.
是假命题 D.
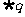 是假命题
是假命题
项中,只有一项是符合题目要求的.
1、已知集合 ,
, ,则
,则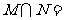 ( ▲ )
( ▲ )
A.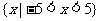 B.
B.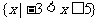
 C.
C.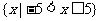 D.
D.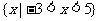

22、(本小题16分)已知函数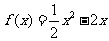 ,
,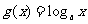 。如果函数
。如果函数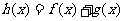 没有极值点,且
没有极值点,且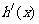 存在零点。(1)求
存在零点。(1)求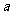 的值;(2)判断方程
的值;(2)判断方程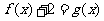 根的个数并说明理由;(3)设点
根的个数并说明理由;(3)设点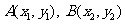
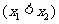 是函数
是函数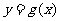 图象上的两点,平行于AB 的切线以
图象上的两点,平行于AB 的切线以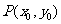 为切点,求证:
为切点,求证: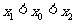 。
。
解:(1)依题意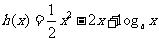 ,
,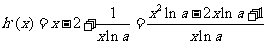

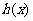 无极值,
无极值,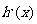 存在零点
存在零点
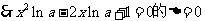 ,
,
 .................(5分)
.................(5分)
(2)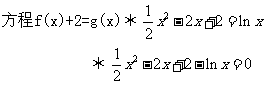
设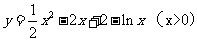
由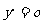 得
得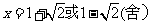
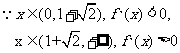
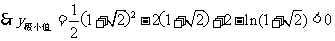
又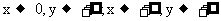
 方程
方程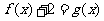 有两个根。
.................(10分)
有两个根。
.................(10分)
(3)由已知: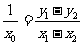 ,所以
,所以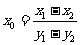 ,
,
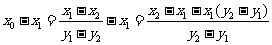 =
=
设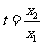 得:
得: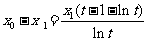
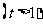 。构造函数
。构造函数
当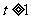 时,
时,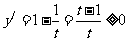 ,所以函数
,所以函数 在当
在当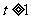 时是增函数
时是增函数
所以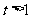 时,
时,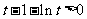 ,所以
,所以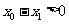 得
得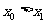 成立
成立
同理可得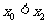 成立,所以
成立,所以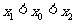 .................(16分)
.................(16分)
20、(本小题共14分)设函数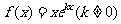 .
.
(Ⅰ)求曲线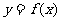 在点
在点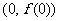 处的切线方程;(Ⅱ)求函数
处的切线方程;(Ⅱ)求函数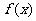 的单调区间;
的单调区间;  (Ⅲ)若函数
(Ⅲ)若函数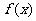 在区间
在区间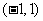 内单调递增,求
内单调递增,求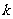 的取值范围.
的取值范围.
解:(Ⅰ)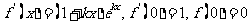 ,
,
曲线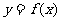 在点
在点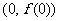 处的切线方程为
处的切线方程为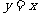 ............(4分)
............(4分)
(Ⅱ)由 ,得
,得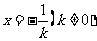 ,...........(5分)
,...........(5分)
若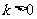 ,则当
,则当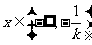 时,
时,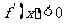 ,函数
,函数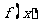 单调递减,
单调递减,
当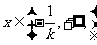 时,
时,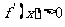 ,函数
,函数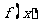 单调递增,...........(7分)
单调递增,...........(7分)
若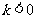 ,则当
,则当 时,
时,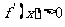 ,函数
,函数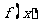 单调递增,
单调递增,
当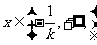 时,
时,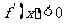 ,函数
,函数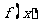 单调递减,...........(9分)
单调递减,...........(9分) 

(Ⅲ)由(Ⅱ)知,若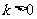 ,则当且仅当
,则当且仅当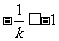 ,即
,即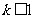 时,函数
时,函数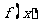 在
在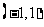 内单调递增;
...........(11分)
内单调递增;
...........(11分)
若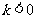 ,则当且仅当
,则当且仅当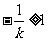 ,即
,即 时,函数
时,函数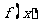 在
在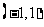 内单调递增,...(13分)
内单调递增,...(13分)

 综上可知,函数
综上可知,函数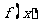 在区间
在区间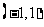 内单调递增时,
内单调递增时,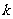 的取值范围是
的取值范围是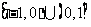 .(14分)
.(14分)
|
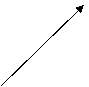 21、(本小题14分)如图,设Ox,Oy是平面内相交成60°角的两条数轴,
21、(本小题14分)如图,设Ox,Oy是平面内相交成60°角的两条数轴,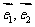 分别是与x轴,y轴正方向同向的单位向量,若
分别是与x轴,y轴正方向同向的单位向量,若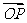 =x
=x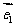 +y
+y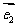 ,则把有序数对(x,y)叫作
,则把有序数对(x,y)叫作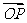 在坐标系xOy中的坐标。假设
在坐标系xOy中的坐标。假设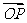 的坐标为(-3,2),
的坐标为(-3,2),
|
|
 (1)计算 |
(1)计算 |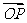 |的大小;
|的大小;
(2)若P1(2,1),求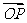 与
与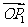 的夹角。
的夹角。
 .................(6分)
.................(6分)
 .................(14分)
.................(14分)
19、(本小题14分)已知函数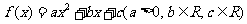
(1)若函数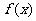 的最小值是
的最小值是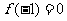 ,且
,且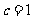 ,
,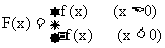 ;
;
求 的值:
的值:
(2)若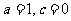 ,且
,且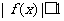 在区间
在区间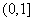 恒成立,试求
恒成立,试求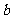 取范围;
取范围;
解(1)由已知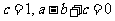 ,且
,且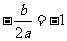
解得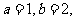
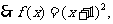
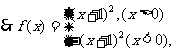 ........(5分)
........(5分)
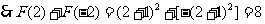 .................(7分)
.................(7分)
(2)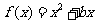 ,原命题等价于
,原命题等价于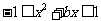 在
在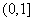 恒成立
恒成立
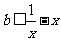 且
且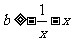 在
在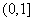 恒成立 .................(10分)
恒成立 .................(10分)
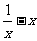 的最小值为0 .................(13分)
的最小值为0 .................(13分)
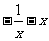 的最大值为
的最大值为
所以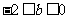 .................(14分)
.................(14分)
18、(本小题14分)已知向量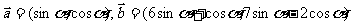 ,设函数
,设函数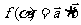 .
.
(Ⅰ)求函数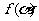 的最大值;
的最大值;
(Ⅱ)在锐角三角形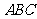 中,角
中,角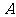 、
、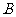 、
、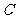 的对边分别为
的对边分别为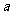 、
、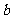 、
、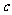 ,
,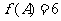 ,
且
,
且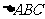 的面积为
的面积为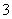 ,
,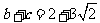
 ,求
,求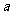 的值.
的值.
解:(Ⅰ)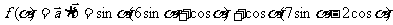
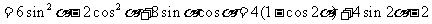 ........(5分)
........(5分)
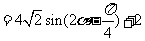
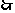
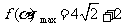 ........................................(7分)
........................................(7分)
(Ⅱ)由(Ⅰ)可得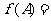
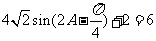 ,
,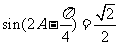
因为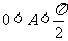 ,所以
,所以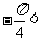
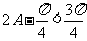 ,
,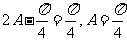 ...........(9分)
...........(9分)
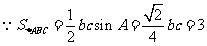
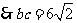 ,又
,又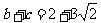 ...........(11分)
...........(11分)
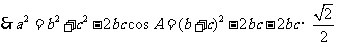
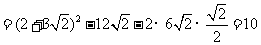
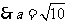 ...................(14分)
...................(14分)
17. 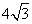
15. (2) 16. 4
13. _1.6__
14.
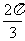
11. 90°
12. 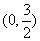
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com