(三)练习

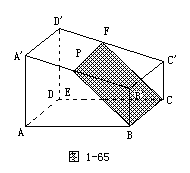
例2　 有一块木料如图1-65，已知棱BC平行于面A′C′．要经过木料表面A′B′C′D′ 内的一点P和棱BC将木料锯开，应怎样画线？所画的线和面AC有什么关系？

解：(1)∵BC∥面A′C′，面BC′经过BC和面A′C′交于B′C′，

∴BC∥B′C′．

经过点P，在面A′C′上画线段EF∥B′C′，由公理4，得：EF∥BC．

的线．

(2)∵EF∥BC，根据判定定理，则EF∥面AC；BE、CF显然都和面AC相交．

总结：解题时，应用直线和平面平行的性质定理，要注意把线面平行转化为线线平行．

练习：(P．22中练习3)

在例题的图中，如果AD∥BC，BC∥面A′C′，那么，AD和面BC′、面BF、面A′C′都有怎样的位置关系．为什么？

∥面BC′．同理AD∥面BF．

又因为BC∥面A′C′，过BC的面EC与面A′C′交于EF，

(二)直接证法

∵a∥α，

∴a与α没有公共点．

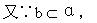
∴a与b没有公共点．

a和b同在平面β内，又没有公共点，

∴a∥b．

下面请同学们完成例题与练习．

(二)直线和平面平行的性质

师：命题“若直线a平行于平面α，则直线a平行于平面α内的一切直线．”对吗？(幻灯显示)

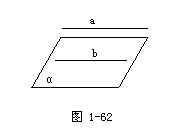
生：不对．

师：为什么不对？(出示教具演示)

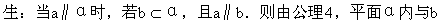
平行的所有直线(为b′，b″)都与a平行(有无数条)，否则，都与a是异面直线．

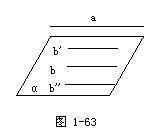
师：在上面的论述中，平面α内的直线b满足什么条件时，可以与直线a平行呢？我们有下面的性质．

直线和平面平行的性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行．

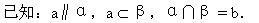
求证：a∥b．

师提示：要证明同一平面β内的两条直线a、b平行，可用反证法，也可用直接证法．

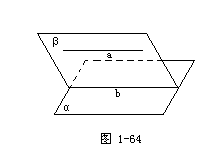
证明：(一)反证法．

假设直线a不平行于直线b．

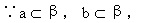
∴ 直线a与直线b相交，假设交点为O，则a∩b＝O．

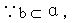
∴a∩α＝O，这与“a∥α”矛盾．

∴a∥b．

1．7直线和平面的位置关系和1．8直线和平面平行的判定与性质这两个课题安排为2课时，本节课为第二课时，讲解直线和平面平行的性质定理．

2．教学难点：直线和平面平行的性质定理的证明及应用．

理4，平面α内与b平行的所有直线都与a平行(有无数条)．否则，都与a是异面直线．

1．教学重点：直线和平面平行的性质定理．

(三)德育渗透点

让学生认识到研究直线和平面平行的性质定理是实际生产的需要，充分体现了理论联系实际的原则．

(二)能力训练点

用转化的方法掌握应用直线与平面平行的性质定理，即由线面平行可推得线线平行．

(一)知识教学点

直线和平面平行的性质定理．