练习册

  • 练习册
  • 试题
     0  253057  253065  253071  253075  253081  253083  253087  253093  253095  253101  253107  253111  253113  253117  253123  253125  253131  253135  253137  253141  253143  253147  253149  253151  253152  253153  253155  253156  253157  253159  253161  253165  253167  253171  253173  253177  253183  253185  253191  253195  253197  253201  253207  253213  253215  253221  253225  253227  253233  253237  253243  253251  447090 
    32.
    　
    (12.0分) 设集合M＝{a|a＝x2－y2，x、y∈Z}，求证：
    (1)一切奇数属于M；
    (2)4k－2(k∈Z)不属于M；
    (3)M中任意两个数的乘积仍属于M．

    试题详情

    24.
    　
    (12.0分) 若A＝{x|x2－ax+a2－19＝0}，B＝{x|x2－5x+6＝0}，C＝{x|x2+2x－8＝0}．
    (1)A∩B＝A∪B，求a的值；
    (2)若A∩B，A∩C＝，求a的值．

    25.
    　
    (12.0分) 集合A＝{x|x＝3n+1，n∈Z}，B＝{x|x＝3n+2，n∈Z}，D＝{x|x＝6n+3，n∈Z}．
    (1)若d∈D，求证：必存在a∈A，b∈B，使d＝a+b；
    (2)对任意的a∈A，b∈B，是否一定有a+b∈D？证明你的结论．

    26.
    　
    (12.0分) 已知集合A＝{x|x2+4x＝0}，集合B＝{x|x2+2(a+1)x+a2－1＝0}，其中x∈R．
    (1)若A∩B＝B，求实数a的取值范围；
    (2)若A∪B＝B，求实数a的值．

    27.
    　
    (12.0分) 已知函数f(x)＝3x3+2x，
    (1)求f(2)、f(－2)、f(2)+f(－2)的值；
    (2)求f(a)、f(－a)、f(a)+f(－a)的值；
    (3)你从(2)中发现了什么结论？

    28.
    　
    (12.0分) 已知函数f(x)＝求f()的值．

    29.
    　
    (12.0分) 求函数y＝的定义域．

    30.
    　
    (12.0分) 函数r＝f(p)的图像如下图所示．

    (1)函数r＝f(p)的定义域可能是什么？
    (2)函数r＝f(p)的值域可能是什么？
    (3)r的哪些值只与p的一个值对应？

    31.
    　
    (12.0分) 如图所示，动点P从边长为4的正方形ABCD的顶点B开始，顺次经C、D、A绕边界运动，用x表示点P的行程，y表示△APB的面积，求函数y＝f(x)的解析式．

    试题详情

    22.
    　
    　
    (10分) 已知三个集合A＝{x|x2－3x+2＝0}，B＝{x|x2－ax+(a－1)＝0}，C＝{x|x2－bx+2＝0}，问同时满足BA，CA的实数a、b是否存在？若存在，求出a、b所有值；若不存在，请说明理由．

    23.
    　
    (12.0分) 设集合A＝{x|x2－3x+2＝0}，B＝{x|2x2－ax+2＝0}，若A∪B＝A，求实数a的值．

    试题详情

    17.
    　
    (4.0分) 若a＜0＜b＜|a|，A＝{x|a≤x≤b，x∈R}，B＝{x|－b≤x≤－a，x∈R}，则A∩B＝________，A∪B＝________．

    18.
    　
    (4.0分) 设全集为U，用集合A、B、C的交、并、补集符号表示图中的阴影部分．

    (1)________；(2)________．

    19.
    　
    (4.0分) 已知定义在R上的函数f(x)的图象关于点对称，且满足，又f(－1)＝1，f(0)＝－2，则f(1)+f(2)+f(3)+…+f(2008)＝________．

    20.
    　
    (4.0分) 已知函数f(x)的图像如图所示，则f(x)的解析式是________．

    21.
    　
    (4.0分) 设I＝{1，2，3，4}，A与B是I的子集，若A∩B＝{1，3}，则称(A，B)为一个“理想配集”，那么符合此条件的“理想配集”的个数是(规定(A，B)与(B，A)是不同的“理想配集”)________．

    试题详情

    1.
    　
    　
    下列命题中真命题的个数为
    ①方程+|y+2|＝0的解集为{2，－2}
    ②集合{y|y＝x2－1，x∈R}与{y|y＝x－1，x∈R}的公共元素所组成的集合是{0，1}
    ③集合{x|x－1＜0}与集合{x|x＞a，a∈R}没有公共元素
    [　]
    A．
    		 0
    B．
    		 1
    C．
    		 2
    D．
    		 3

    2.
    　
    　
    设a、b、c为非零实数，则M＝的所有值组成的集合为
    [　]
    A．
    		 {4}
    B．
    		 {－4}
    C．
    		 {4，－4，0}
    D．
    		 {0}

    3.
    　
    　
    设集合P＝{x|x2+2x－8＝0}，Q＝{x|ax+1＝0}，若QP，则实数a可取不同值的个数为
    [　]
    A．
    		 1
    B．
    		 2
    C．
    		 3
    D．
    		 4

    4.
    　
    　
    设M＝{x|x＝a2+1，a∈N+}，P＝{y|y＝b2－4b+5，b∈N+}，则下列关系正确的是
    [　]
    A．
    		 M＝P
    B．
    		 MP
    C．
    		 PM
    D．
    		 M∈P

    5.
    　
    　
    已知集合P＝{x|x＝n，n∈Z}，Q＝{x|x＝，n∈Z}，R＝{x|x＝+n，n∈Z}，则下列各式正确的是
    [　]
    A．
    		 QP
    B．
    		 Q＝P∪R
    C．
    		 QR
    D．
    		 Q＝P∩R

    6.
    　
    已知非空集合P、Q，定义P－Q＝{x|x∈P，但xQ}，则P－(P－Q)等于
    [　]
    A．
    		 P
    B．
    		 Q
    C．
    		 P∩Q
    D．
    		 P∪Q

    7.
    　
    2006年寒假，小明为完成社会实践作业，对某校大学生进行调查，结果如下：电脑拥有率为49%，手机拥有率为85%，MP3拥有率为44%，拥有上述三种物品中两种的占38%，三种物品齐全的占25%，那么三种物品中一种也没有的大学生比例为
    [　]
    A．
    		 10%
    B．
    		 12%
    C．
    		 15%
    D．
    		 27%

    8.
    　
    设A、B、I均为非空集合，且满足ABI，则下列各式中错误的是
    [　]
    A．
    		 (A)∪B＝I
    B．
    		 (A)∪(B)＝I
    C．
    		 A∩(B)＝
    D．
    		 (A)∩(B)＝B

    9.
    　
    已知集合A、B、C满足条件A∪B＝A∪C，则下列各式一定成立的是
    [　]
    A．
    		 B＝C
    B．
    		 A∩B＝A∩C
    C．
    		 (A)∩B＝(A)∩C
    D．
    		 A∩(B)＝A∩(C)

    10.
    　
    集合P＝{1，4，9，16，…n2，…}，若对于运算“*”“a∈P，b∈P，则a*b∈P”，则运算“*”可以是
    [　]
    A．
    		 加法
    B．
    		 减法
    C．
    		 除法
    D．
    		 乘法

    11.
    　
    设f(x)＝|x－1|－|x|，则f[f()]等于
    [　]
    A．
    B．
    		 0
    C．
    D．
    		 1

    12.
    　
    下列图形中，不可能是函数y＝f(x)的图像的是
    [　]
    A．
    B．
    C．
    D．

    13.
    　
    设M＝{x|－2≤x≤2}，N＝{y|0≤y≤2}，给出下列4个图形，其中能表示以集合M为定义域，N为值域的函数关系是
    [　]
    A．
    B．
    C．
    D．

    14.
    　
    设集合A＝{x|0≤x≤2}，B＝{y|1≤y≤2}，在下图所示的图形中，能表示从集合A到集合B的映射的是
    [　]
    A．
    B．
    C．
    D．

    15.
    　
    下列哪一个对应是一个集合P到集合S的映射
    [　]
    A．
    		 P＝{有理数}，S＝{数轴上的点}，对应法则f：有理数→数轴上的点
    B．
    		 P＝{数轴上的点}，S＝{有理数}，对应法则f：数轴上的点→有理数
    C．
    		 x∈P＝R，y∈S＝{x|x＞0}，对应法则f：x→y＝|x|
    D．
    		 x∈P＝{x|x≤0}，y∈S＝{x|x＞0}，对应法则f：x→y＝x2

    16.
    　
    某地一天内的气温Q(t)(单位：℃)与时刻t(单位：时)之间的关系如图所示，令C(t)表示时间段[0，t]内的温差(即时间段[0，t]内最高温度与最低温度的差)．C(t)与t之间的函数关系用下列图像表示，则正确的图像大致是
    [　]
    A．
    B．
    C．
    D．

    第II卷 主观题

    17
    		 18
    		 19
    		 20
    		 21
    		 22
    		 23
    		 24
    		 25
    		 26
    　
    		 　
    		 　
    		 　
    		 　
    		 　
    		 　
    		 　
    		 　
    		 　
    27
    		 28
    		 29
    		 30
    		 31
    		 32
    		 　
    		 　
    		 　
    		 　
    　
    		 　
    		 　
    		 　
    		 　
    		 　
    		 　
    		 　
    		 　
    		 　

    试题详情

    19.一船在海面A处望见两灯塔P、Q在北15°西的一条直线上.该船沿东北方向航行4海里到达B处，望见灯塔P在正西方向，灯塔Q在西北方向，求两灯塔距离.

    解：如图，由题意可知：

    ∠A＝45°+15°=60°，

    ∠ABP＝45°，∠PBQ＝45°

    ∴∠ABQ＝90°

    ∴∠AQB＝30°，∠APB＝75°

    sin75°＝sin(45°+30°)＝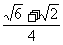

    在△ABP中，AB＝4，由正弦定理知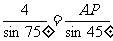

    ∴AP＝4(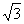－1)

    在△ABQ中，∠ABQ＝90°，AB＝4

    ∴AQ＝8

    ∴PQ＝AQ－AP＝8－4(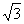－1)＝12－4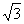

    故两灯塔P、Q的距离为12－4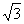海里.

    试题详情

    18.如图，已知△ABC中，D、E、F分别是BC、CA、AB的中点，求证：

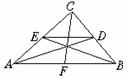
    (1)∥；

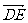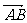    (2)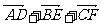＝0.

    证明：(1)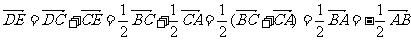

    ∴∥

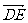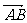
    (2)

    ∴

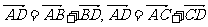
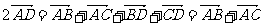
    同理可得

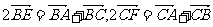
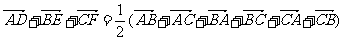    ∴＝0

    试题详情

    17.已知a＝(2x－y+1，x+y－2)，b＝(2，－2)，当x，y为何值时(1)a＝b (2)a∥b

    解：(1)由题意可知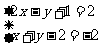：，解得

    (2)由向量共线条件知：－2(2x－y+1)－2(x+y－2)＝0

    化简得：3x－1＝0

    试题详情

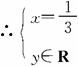
    16.已知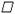ABCD的顶点A的坐标为(－2，1)，一组对边AB、CD的中点分别为M(3，0)、N(－1，－2).求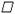ABCD的其余顶点坐标.

    解：略

    试题详情

    15.已知点A(0，2)、B(1，－1)、C(2，－4)，求证：A、B、C三点共线.

    证明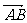：∵＝(1－0，－1－2)＝(1，－3).

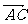    ＝(2－0，－4－2)＝(2，－6)

    又1×(－6)－2×(－3)＝0，

    ∴∥

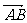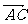
    又直线AB、直线AC有公共点A

    ∴A、B、C三点共线.

    试题详情


    同步练习册答案