
2.(2008山东卷, 24) Thank you for all your hard work last week. I don’t think we ____ it without you.
A. can manage B. could have managed
C. could manage D. can have managed
 [解析]
B 此题考查情态动词表示虚拟意义的用法。I
don’t think…是否定前移。意为:我认为没有你我们本不能做成这件事的。此题关键是要根据句意知道是虚拟语气,其基本形式是情态动词(过去式)+have
done,所以其他选项皆可排除。
[解析]
B 此题考查情态动词表示虚拟意义的用法。I
don’t think…是否定前移。意为:我认为没有你我们本不能做成这件事的。此题关键是要根据句意知道是虚拟语气,其基本形式是情态动词(过去式)+have
done,所以其他选项皆可排除。
[答案]B
3(09福建). But for the help of my English teacher, I____the first prize in the English Writing Competition.
A. would not win B. would not have won C. would win D. would have won
[答案]B 虚拟语气。此处虚拟语气表示与过去事实相反,句子谓语动词用would/should/could/might + have done结构,故选B。
1.(2007 全国卷II, 8) _______ he had not hurt his leg, John would have won the race.
A. If B. Since C. Though D. When
[解析]A 有题干可知,“若不是他伤了腿,约翰就能赢得比赛了”,运用了虚拟语气,故用if。
|
课题:函数的最值 |
三、求函数最值的方法: |
|
一、最值的定义 |
1. |
|
最大值:…… |
2. |
|
最小值:…… |
3. |
|
二、点拔与说明 |
4. |
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
3. 利用单调性求最值的解答题,单调性的理由要用定义法书写。
2.求函数求最值的方法
(1)图像法(2)二次函数法(3)单调性法(4)求值域法
1.最值的定义及几何特征。
(三)新课学习
1.最大值、最小值的定义
最大值:设函数y=f(x)定义域为I,如果存在实数M满足:
(1) 对于I中任意的x,都有f (x)<=M;
(2) I中存在一个数x0使得f(x0)=M。
则称M是函数y=f(x)的最大值,记作f(x)max=f(x0)=M
最小值:设函数y=f(x)定义域为I,如果存在实数M满足:
(3) 对于I中任意的x,都有f(x)>=M;
(4) I中存在一个数x0使得f(x0)=M。
则称M是函数y=f(x)的最小值,记作f(x)min=f(x0)=M
2.点拨与说明
(1)函数最值的图形特征:函数的最大(小)值是函数图像上最高(低)点的纵坐标。
(2)二次函数y=ax2+bx=c (a不为0)的最值:
①a<0,当x=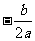 时,
时,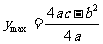 。
。
②a>0,当x= 时,
时,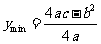 。
。
(3)若f(x)在[a,b]上为增函数,则f(x)min=f(a), f(x)max=f(b);
若f(x)在[a,b]上为减函数,则f(x)min=f(b), f(x)max=f(a)。
(4) 若f(x)值域为[a,b],则f(x)min=a, f(x)max=b。
3.求函数最值的方法
根据以上的点拨与说明,我们要求函数的最值可以用什么方法?
(1)图像法(2)二次函数法(3)单调性法(4)求值域法
4.反复实践,认识升华
课本例3教学。
对应练习1:(1)函数y=-x2+2x的最大值为 。
(2)函数y=-x2+2x (2=<x=<3)的最大值为 。
说明:(1)分组讨论,合作交流完成。
(2)思考两题的结果为什么不同。
(3)当二次函数的定义域被限制时,如何求最值。
课本例4教学
说明:利用单调性求最值的解答题,单调性的理由要用定义法书写。
对应练习2:求函数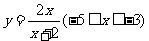 的最大值和最小值。
的最大值和最小值。
(请两位成绩较好的学生板演,其他学生在下面做)
(二) 创设情境、引入新知
请几位学生画下列函数的图像:
(1) y=-x+1 (2)y=-x+1 , x>-1 (3)y=-x+1 , x>=-1
(4) y=-x+1 , x=-1,0,1 (5)y=--x2-2 (6)y=1/x

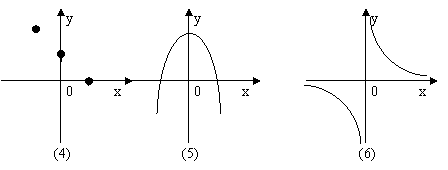
观察以上图像,哪些函数有最大值?由此你能归纳出最大值的定义吗?
(学生观察、比较,用自己的语言描述最大值的定义)
(一) 复习提高、巩固旧知
问题:1.单调函数的定义是什么?有怎样的图形特征?
2.寻找函数单调区间或判断单调性有哪几种方法?
3.用定义法证明单调性有哪几个步骤?
重点:函数最值的定义与求法。
难点:如何求一个具体函数的最值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com