
(一) 选择题
1、下列函数中,既是(0,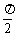 )上的增函数,又是以π为周期的偶函数是
)上的增函数,又是以π为周期的偶函数是
A、y=lgx2 B、y=|sinx| C、y=cosx D、y=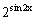
1、
如果函数y=sin2x+acos2x图象关于直线x=-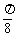 对称,则a值为
对称,则a值为
A、
-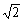 B、-1
C、1
D、
B、-1
C、1
D、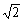
3、函数y=Asin(ωx+φ)(A>0,φ>0),在一个周期内,当x=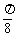 时,ymax=2;当x=
时,ymax=2;当x= 时,ymin=-2,则此函数解析式为
时,ymin=-2,则此函数解析式为
A、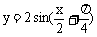 B、
B、
C、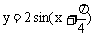 D、
D、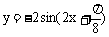
4、已知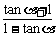 =1998,则
=1998,则 的值为
的值为
A、1997 B、1998 C、1999 D、2000
5、已知tanα,tanβ是方程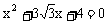 两根,且α,β
两根,且α,β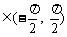 ,则α+β等于
,则α+β等于
A、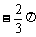 B、
B、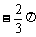 或
或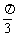 C、
C、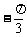 或
或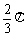 D、
D、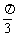
6、若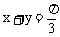 ,则sinx·siny的最小值为
,则sinx·siny的最小值为
A、-1 B、-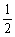 C、
C、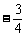 D、
D、
7、函数f(x)=3sin(x+100)+5sin(x+700)的最大值是
A、5.5 B、6.5 C、7 D、8
8、若θ∈(0,2π],则使sinθ<cosθ<cotθ<tanθ成立的θ取值范围是
A、(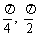 ) B、(
) B、(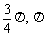 ) C、(
) C、(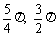 ) D、(
) D、(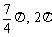 )
)
9、下列命题正确的是
A、 若α,β是第一象限角,α>β,则sinα>sinβ
B、
函数y=sinx·cotx的单调区间是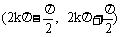 ,k∈Z
,k∈Z
C、
函数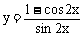 的最小正周期是2π
的最小正周期是2π
D、
函数y=sinxcos2φ-cosxsin2x的图象关于y轴对称,则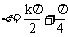 ,k∈Z
,k∈Z
10、 函数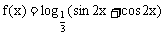 的单调减区间是
的单调减区间是
A、
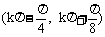 B、
B、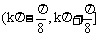
B、
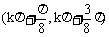 D、
D、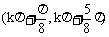 k∈Z
k∈Z
例1、 已知函数f(x)=
(1) 求它的定义域和值域;
(2) 求它的单调区间;
(3) 判断它的奇偶性;
(4) 判断它的周期性。
分析:
(1)x必须满足sinx-cosx>0,利用单位圆中的三角函数线及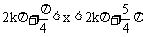 ,k∈Z
,k∈Z
∴ 函数定义域为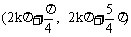 ,k∈Z
,k∈Z
 ∵
∵ 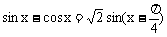
∴ 当x∈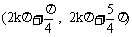 时,
时,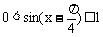
∴ 
∴ 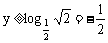
∴ 函数值域为[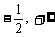 )
)
(3)∵ f(x)定义域在数轴上对应的点关于原点不对称
∴ f(x)不具备奇偶性
(4)∵ f(x+2π)=f(x)
∴ 函数f(x)最小正周期为2π
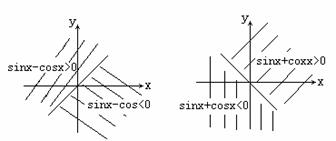
注;利用单位圆中的三角函数线可知,以Ⅰ、Ⅱ象限角平分线为标准,可区分sinx-cosx的符号;
以Ⅱ、Ⅲ象限角平分线为标准,可区分sinx+cosx的符号,如图。
例2、 化简 ,α∈(π,2π)
,α∈(π,2π)
分析:
凑根号下为完全平方式,化无理式为有理式
∵ 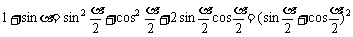
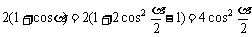
∴ 原式=
∵ α∈(π,2π)
∴ 
∴ 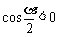
当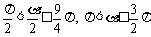 时,
时,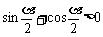
∴ 原式=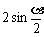
当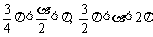 时,
时,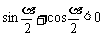
∴ 原式=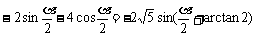
∴ 原式=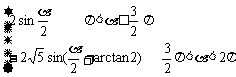
注:
1、本题利用了“1”的逆代技巧,即化1为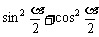 ,是欲擒故纵原则。一般地有
,是欲擒故纵原则。一般地有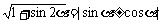 ,
,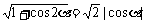 ,
, 。
。
2、三角函数式asinx+bcosx是基本三角函数式之一,引进辅助角,将它化为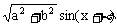 (取
(取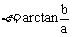 )是常用变形手段。特别是与特殊角有关的sin±cosx,±sinx±
)是常用变形手段。特别是与特殊角有关的sin±cosx,±sinx±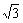 cosx,要熟练掌握变形结论。
cosx,要熟练掌握变形结论。
例3、 求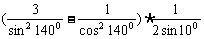 。
。
分析:
原式=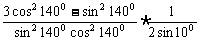
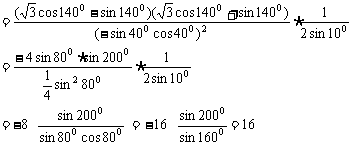
注:在化简三角函数式过程中,除利用三角变换公式,还需用到代数变形公式,如本题平方差公式。
例4、已知00<α<β<900,且sinα,sinβ是方程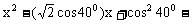
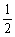 =0的两个实数根,求sin(β-5α)的值。
=0的两个实数根,求sin(β-5α)的值。
分析:
由韦达定理得sinα+sinβ=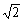 cos400,sinαsinβ=cos2400-
cos400,sinαsinβ=cos2400-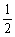
∴ sinβ-sinα=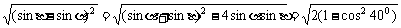
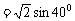
又sinα+sinβ=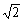 cos400
cos400
∴ 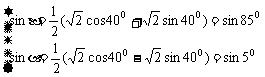
∵ 00<α<β< 900
∴ 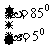
∴ sin(β-5α)=sin600=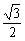
注:利用韦达定理变形寻找与sinα,sinβ相关的方程组,在求出sinα,sinβ后再利用单调性求α,β的值。
例5、(1)已知cos(2α+β)+5cosβ=0,求tan(α+β)·tanα的值;
(2)已知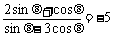 ,求
,求 的值。
的值。
分析:
(1) 从变换角的差异着手。
∵ 2α+β=(α+β)+α,β=(α+β)-α
∴ 8cos[(α+β)+α]+5cos[(α+β)-α]=0
展开得:
13cos(α+β)cosα-3sin(α+β)sinα=0
同除以cos(α+β)cosα得:tan(α+β)tanα=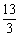
(2) 以三角函数结构特点出发
∵ 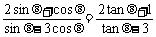
∴ 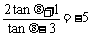
∴ tanθ=2
∴ 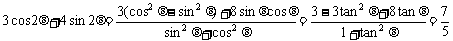
注;齐次式是三角函数式中的基本式,其处理方法是化切或降幂。
例6、已知函数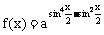 (a∈(0,1)),求f(x)的最值,并讨论周期性,奇偶性,单调性。
(a∈(0,1)),求f(x)的最值,并讨论周期性,奇偶性,单调性。
分析:
对三角函数式降幂
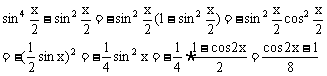
∴ f(x)=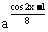
令 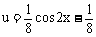
则 y=au
∴ 0<a<1
∴ y=au是减函数
∴ 由 得
得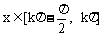 ,此为f(x)的减区间
,此为f(x)的减区间
由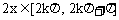 得
得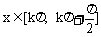 ,此为f(x)增区间
,此为f(x)增区间
∵ u(-x)=u(x)
∴ f(x)=f(-x)
∴ f(x)为偶函数
∵ u(x+π)=f(x)
∴ f(x+π)=f(x)
∴ f(x)为周期函数,最小正周期为π
当x=kπ(k∈Z)时,ymin=1
当x=kπ+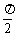 (k∈Z)时,ynax=
(k∈Z)时,ynax=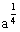
注:研究三角函数性质,一般降幂化为y=Asin(ωx+φ)等一名一次一项的形式。
练习
19.孔子云“仁者乐山,智者乐水。”大自然造就了人,也陶冶着人,改变着人。陆游为梅花填词,想到了孤芳自赏;毛泽东为梅花填词,想到了无产阶级革命者的情怀。一个人在面临挫折,意志消沉时,看到翱翔雄鹰,也许会增添生活的勇气;一个人在心灰意冷时,看到浩瀚大海,,也许会豁然开朗,壮志满怀。请你回想自己类似的经历,以“来自自然的启迪”为题写一篇文章。
要求:立意自定,文体自选,不少于800字。
语文评分标准
 一等(40-36分):立意较深,中心突出,内容充实,结构严密,语言通畅。
一等(40-36分):立意较深,中心突出,内容充实,结构严密,语言通畅。
二等(35-31分):中心明确,内容充实,结构完整,语言通顺。
三等(30-24分):中心尚明确,内容较具体,结构完整,语言基本通顺。
四等(23-16分):中心欠明确,内容空泛,结构基本完整,语病较多。
五等(15分以下):完全离题,或感情不健康,或文理混乱,或语病严重,或不足300字,不成篇。
说明:① 构思新颖有创造,或语言生动有文采,或书写美观端正、卷面整洁,酌加2
-3分。 ② 错别字3个扣1分(重出不计)。③ 不足600字,降等给分。
(二)我的四季
张洁
秋天,我和别人一样收获。望着我那干瘪的谷粒,心里有一种又酸又苦的欢乐。但我并不因我的谷粒比别人干瘪便灰心或丧气。我把它们捧在手里,紧紧地贴近心窝,仿佛那是新诞生的一个自我。
富有而善良的邻人,感叹我收获的微少,我却疯人一样地大笑。在这笑声里,我知道我已成熟。我已有了一种特别的量具,它不量谷物只量感受。 我的邻人不知和谷物同时收获的还有人生。 我已经爱过,恨过,欢笑过,哭泣过,体味过,彻悟过……细细想来,便知晴日多于阴雨,收获多于劳作。只要我认真地活过,无愧地付出过,人们将无权耻笑我是入不敷出的傻瓜,也不必用他的尺度来衡量我值得或是不值得。
16.如何理解“我”的欢乐是“又酸又苦”?(2分)
17.文中“我”捧着“干瘪的谷粒”为什么没有灰心和丧气?(2分)
18.如何理解文章最后画线句子的哲理意义。(2分)
6.在横线处填写恰当的句子,构成前后连贯、合理的排比句。(4分)
人的一生像金,要刚正,人格须挺立;人的一生像木,要正直,立场须坚定;______________ ,_________ ,______________; ______________ ,_________ ,______________;人的一生像土,要本色,作风须朴实。
5.补出下列各句中的空缺部分。(共6分) 
(1)恰同学少年, ;书生意气, 。 (《沁园春·长
沙》)
(2)故木受绳则直,金就砺则利,
,
。(《荀子·劝学》)
(3)锲而舍之,朽木不折
,
。(荀子《劝学》)
(4)生乎吾后,
,
。(韩愈《师说》)
(5)是故无贵无贱,无长无少,
,
。(韩愈《师说》)
(6) , ,如是而已。 (韩愈《师说》)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com