
[例1]读“环境、资源和人口关系示意图”,回答1-2题。

1.图中字母F、G、H代表的含义分别是
A.资源开发、产品消费、废物排放B.产业活动、产品消费、废物排放
C.产品消费、废物排放、产业活动D.资源开发、产业活动、产品消费
2.E过程可能出现的问题是
①过度开发导致可再生资源遭到破坏 ②过度排放污染物超过环境的自净能力 ③生产过程导致工农业污染排放④资源开采导致环境的污染和生态破坏
A.①② B.②③ C.①④ D.③④
解析:本题主要是考查人类社会和环境之间的关系,其中E表示环境为人类社会提供资源,F表示生产活动,G表示人类消费各种产品,H表示人类产生的废弃物排放到环境中去;由于E过程表示从环境中获取资源,如果获取资源的速度超过了资源的再生能力就会产生环境问题,其中环境问题包括环境污染和生态破坏。
答案: 1.B 2.C
[例2]2009年12月19日,有190多个国家参与的哥本哈根气候变化会议在经历复杂曲折的协商后,发表了《哥本哈根协议》。根据图甲至图丙回答下列问题问题。

图甲 欧洲局部区域图

图乙 世界平均气温变化图 图丙 宜昌、武汉近百年平均气温变化图
(1)根据图乙和图丙描述近百年来不同空间尺度气温变化的差异性。
(2)分析全球气候变暖的主要人为原因。
(3)简要说明气候变暖对图甲中甲所在国家的主要影响。
解析:解答第(1)小题时需要答出大空间尺度和小空间尺度的区别,大空间尺度是在波动中上升,小空间尺度有的波动上升有的波动下降;第(2)小题主要要求回答人为原因,必须从二氧化碳含量的增多入手;第(3)小题由于甲是沿海国家,因此海平面上升会导致沿海低地和城市被淹没。
答案:
(1)从全球尺度看,世界气温呈明显上升(波动上升)趋势;就某个城市而言气温变化存在差异,有的波动上升,有的甚至波动下降。(8分)
(2)由于大量燃烧矿物性燃料而过度排放二氧化碳等温室气体;由于破坏森林(毁林)而使吸收的二氧化碳减少。(6分)
(3)海平面上升,淹没沿海低地及城市。(6分)
[例1]“广谷大川异制,民生其间者异俗”(《礼记·王制》),“沃土之民不材,瘠土之民向义”(《管子》),以上都是我国古代有关人地关系的思想,据此回答1-2题。
1.材料中两句话反映的人地关系思想是
A.地理环境决定论 B.人类中心论 C.人地相关论 D.人地伙伴论
2.该思想形成于
A.农业社会时期 B.工业社会时期
C.人类社会早期 D.后工业化时期
解析:第1题中不同的地理环境决定着不同地区的民俗风情;土壤的肥沃程度决定着经济的水平的高低,属于典型的地理环境决定论;第2题中地理环境决定论出现在生产力水平较低的人类社会的早期。
答案: 1.A 2.C
21.(本题满分12分)
设 是圆心在抛物线
是圆心在抛物线 上的一系列圆,它们的圆心的横坐标分别记为
上的一系列圆,它们的圆心的横坐标分别记为 ,已知
,已知 ,又
,又 都与
都与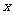 轴相切,且顺序逐个相邻外切。
轴相切,且顺序逐个相邻外切。
(1)求 的值,并求由
的值,并求由 构成的数列
构成的数列 的通项公式;
的通项公式;
(2)求证: 。
。




20.(本题满分12分)
已知抛物线 与直线
与直线 交于
交于 两点,
两点, 为坐标原点。
为坐标原点。
(1)当 ,且直线
,且直线 过抛物线
过抛物线 的焦点时,求
的焦点时,求 的值;
的值;
(2)当直线 的倾斜角之和为45°时,求
的倾斜角之和为45°时,求 之间满足的关系式,并证明直线
之间满足的关系式,并证明直线 过定点。
过定点。
19.(本题满分12分)
 在边长为3的正三角形
在边长为3的正三角形 中,点
中,点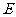 、
、 分别是
分别是 、
、 边上的点,并且满足
边上的点,并且满足 (如图)。将
(如图)。将 沿
沿 折起到
折起到 的位置,使二面角
的位置,使二面角 成直二面角,连结
成直二面角,连结 和
和 。
。
(1)求证: 平面
平面 ;
;
(2)求四棱锥 的体积;
的体积;
(3)在 上是否存在一点
上是否存在一点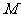 ,使
,使 平面
平面 ,若存在指出
,若存在指出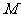 点位置,不存在说明理由。
点位置,不存在说明理由。
18.(本题满分13分)
设函数 图象关于原点对称,且
图象关于原点对称,且 时,
时, 取极小值
取极小值 。
。
(1)求 ;
;
(2)若 时,求证:
时,求证: 。
。
17.(本题满分13分)
甲、乙队按“七场四胜”制进行篮球决赛:即甲或乙队,谁先累计获胜四场比赛就是决赛的冠军。若在每场比赛中,甲队获胜的概率均为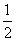 ,且每场比赛必须分出胜负。每场比赛的胜或负不影响其他场次比赛的胜或负。求:
,且每场比赛必须分出胜负。每场比赛的胜或负不影响其他场次比赛的胜或负。求:
(1)甲队在第五场比赛后获得冠军的概率;
(2)甲队获得冠军的概率。
16.(本题满分13分)
已知函数 。
。
(1)求函数 的最小值和单调递增区间;
的最小值和单调递增区间;
(2)设 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、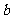 、
、 ,且
,且 ,求边长
,求边长 、
、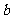 。
。
15.若关于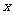 的方程
的方程 有解,则实数
有解,则实数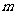 的取值范围是 。
的取值范围是 。
14.为预防和控制甲流感,某学校医务室欲将23支相同的温度计分发到高三年级10个班级中,要求分发到每个班级的温度计不少于2支,则不同的分发方式共有 种。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com