
1.下列加点字注音全部正确的一项是 ( )
A.百舸(gě) 寥廓(liáo) 挥斥方遒(qiú) 浪遏飞舟(è)
B.青荇(xìng) 漫溯(shuò) 笙箫(shēn) 残羹(gēng)
C.罗绮(qĭ) 霉菌(qūn) 发酵(xiào 漪沦(yī)
D.踟蹰(chíchú) 跫音(qióng) 絮语(xù) 懊丧(aŏ)
21. (本题满分14分)
已知实数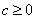 ,曲线
,曲线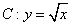 与直线
与直线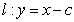 的交点为
的交点为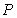 (异于原点
(异于原点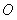 ),在曲线
),在曲线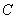 上取一点
上取一点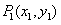 ,过点
,过点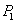 作
作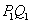 平行于
平行于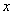 轴,交直线
轴,交直线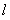 于点
于点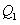 ,过点
,过点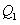 作
作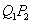 平行于
平行于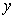 轴,交曲线
轴,交曲线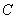 于点
于点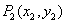 ,接着过点
,接着过点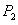 作
作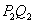 平行于
平行于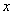 轴,交直线
轴,交直线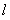 于点
于点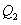 ,过点
,过点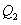 作
作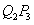 平行于
平行于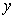 轴,交曲线
轴,交曲线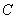 于点
于点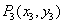 ,如此下去,可以得到点
,如此下去,可以得到点 ,
,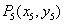 ,…,
,…,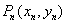 ,… . 设点
,… . 设点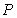 的坐标为
的坐标为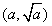 ,
,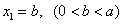 .
.
(Ⅰ)试用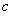 表示
表示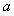 ,并证明
,并证明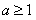 ;
;
(Ⅱ)试证明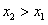 ,且
,且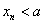 (
(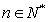 );
);
(Ⅲ)当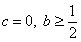 时,求证:
时,求证: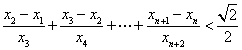 (
(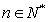 ).
).
20. (本题满分14分)
已知函数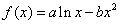 图象上一点
图象上一点 处的切线方程为
处的切线方程为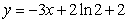 .
.
(Ⅰ)求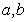 的值;
的值;
(Ⅱ)若方程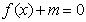 在
在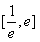 内有两个不等实根,求
内有两个不等实根,求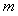 的取值范围(其中
的取值范围(其中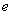 为自然对数的底数);
为自然对数的底数);
(Ⅲ)令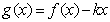 ,若
,若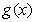 的图象与
的图象与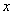 轴交于
轴交于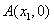 ,
,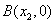 (其中
(其中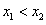 ),
),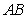 的中点为
的中点为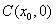 ,求证:
,求证: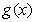 在
在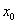 处的导数
处的导数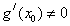 .
.
19. (本题满分14分)
如图,在四棱锥 中,底面
中,底面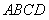 是边长为
是边长为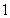 的菱形,
的菱形,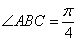 ,
,
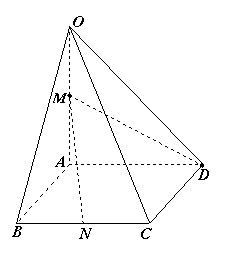
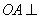 底面
底面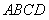 ,
, 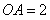 ,
,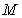 为
为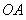 的中点,
的中点,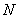 为
为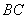 的中点.
的中点.
(Ⅰ)证明:直线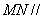 平面
平面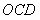 ;
;
(Ⅱ)求异面直线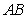 与
与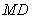 所成角的大小;
所成角的大小;
(Ⅲ)求点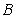 到平面
到平面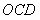 的距离.
的距离.
18. (本题满分14分)
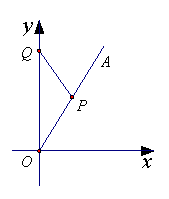 如右图所示,在直角坐标系
如右图所示,在直角坐标系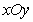 中,射线
中,射线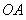 在第一象限,且与
在第一象限,且与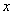 轴的正半轴成定角
轴的正半轴成定角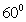 ,动点
,动点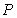 在射线
在射线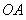 上运动,动点
上运动,动点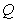 在
在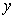 轴的正半轴上运动,
轴的正半轴上运动,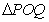 的面积为
的面积为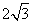 .
.
(Ⅰ)求线段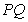 中点
中点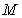 的轨迹
的轨迹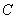 的方程;
的方程;
(Ⅱ)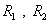 是曲线
是曲线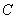 上的动点,
上的动点, 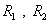 到
到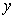 轴的距离之和为
轴的距离之和为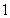 ,
,
设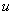 为
为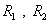 到
到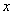 轴的距离之积.问:是否存在最大的常数
轴的距离之积.问:是否存在最大的常数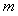 ,
,
使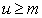 恒成立?若存在,求出这个
恒成立?若存在,求出这个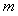 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
17. (本题满分12分)
一个盒子装有六张卡片,上面分别写着如下六个定义域为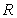 的函数:
的函数:
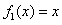 ,
,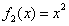 ,
,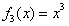 ,
,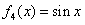 ,
,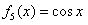 ,
,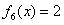 .
.
(Ⅰ)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(Ⅱ)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数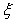 的分布列和数学期望.
的分布列和数学期望.
16. (本题满分12分)
已知函数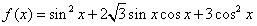 .
.
(Ⅰ)求函数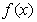 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(Ⅱ)已知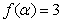 ,且
,且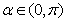 ,求
,求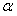 的值.
的值.
(二)选做题(14~15题,考生只能从中选做一题)
14. 已知参数方程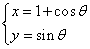 ,(参数
,(参数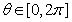 ),则该曲线
),则该曲线
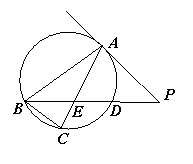 上的点与定点
上的点与定点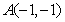 的距离的最小值是
.
的距离的最小值是
. 

15. 如图,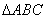 是圆
是圆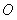 的内接三角形,
的内接三角形, 是圆
是圆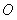
的切线,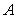 为切点,
为切点,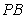 交
交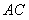 于点
于点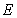 ,交圆
,交圆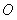
于点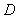 ,若
,若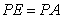 ,
, 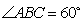 ,且
,且
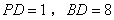 ,则
,则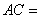 .
.
(一)必做题(9~13题)
9. 设向量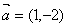 ,
,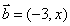 ,若
,若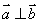 ,则
,则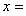 ;
; 

10.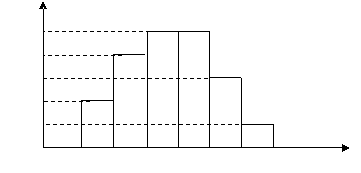 某社会调查机构就某地居民的月收入
某社会调查机构就某地居民的月收入
调查了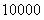 人,并根据所得数据画
人,并根据所得数据画
了样本的频率分布直方图(如右图).
为了分析居民的收入与年龄、学历、
职业等方面的关系,要从这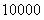 人
人
中再用分层抽样方法抽出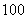 人作进
人作进
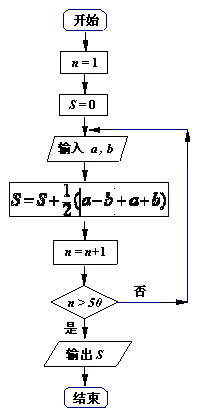 一步调查,则在
一步调查,则在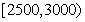 (元)
(元)
的月收入段应抽出 人.
11.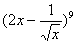 的展开式中,常数项为
;(用数字作答)
的展开式中,常数项为
;(用数字作答)
12. 将 这
这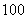 个自然数任意分成
个自然数任意分成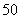 组,每组两个数,
组,每组两个数,
现将每组的两个数中任意一个记为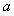 ,另一个数记为
,另一个数记为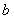 ,按右框图
,按右框图
所示进行运算(注:框图中每次“输入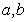 ”为同一组的
”为同一组的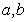 值,
值,
且每组数据不重复输入.),则输出的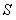 最大值为
;
最大值为
;
13. 已知函数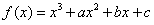 的一个零点为
的一个零点为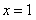 ,
,
另外两个零点可分别作为一个椭圆、一双曲线的离心率,
则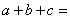 ;
;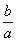 的取值范围是
.
的取值范围是
.
8. 对于任意实数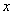 ,符号
,符号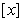 表示不超过
表示不超过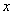 的最大整数,例如:
的最大整数,例如: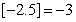 ,
,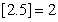 ,
,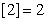 ,那么
,那么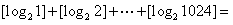 ( )
( )
A.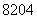 B.
B.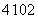 C.
C.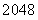 D.
D. 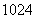
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com