
20.直线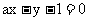 与双曲线
与双曲线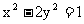 相交于P、Q两点,
(1)当a为何值时,
相交于P、Q两点,
(1)当a为何值时,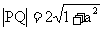 (2)是否存在a值,使得PQ为直径的圆经过原点?若存在,求出a的值;若不存在,给
(2)是否存在a值,使得PQ为直径的圆经过原点?若存在,求出a的值;若不存在,给
出证明。
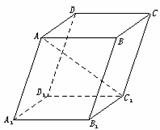
19.如下图,已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为a的正方形,侧棱AA1长为b,且AA1与AB、AD的夹角都是120°.求:
(1)AC1的长;
(2)直线BD1与AC所成的角的余弦值.
18.已知椭圆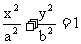 (a>b>0),它的一条准线方程是x=1,倾斜角为45°的直线交椭圆于
(a>b>0),它的一条准线方程是x=1,倾斜角为45°的直线交椭圆于
A、B两点,设AB的中点为M,直线AB与OM的夹角为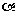
(1)
当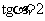 时,求椭圆方程;
时,求椭圆方程;
(2)
当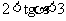 时,证明
时,证明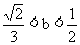
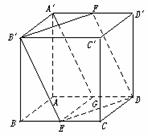
17.在棱长为a的正方体ABCD-A′B′C′D′中,E、F分别是BC、A′D′的中点.
(1)求证:四边形B′EDF是菱形;
(2)求直线A′C与DE所成的角;
(3)求直线AD与平面B′EDF所成的角;
(4)求面B′EDF与面ABCD所成的角(选作)
(5)求B到平面B′EDF的距离
16.已知m、n是直线,α、β、γ是平面,给出下列命题:
①若α⊥β,α∩β=m,n⊥m,则n⊥α或n⊥β; ②若α∥β,α∩γ=m,β∩γ=n,则m∥n;
③若m不垂直于α,则m不可能垂直于α内的无数条直线;
④若α∩β=m,n∥m且n α,n
α,n β,则n∥α且n∥β.
β,则n∥α且n∥β.
其中正确的命题序号是 (注:把你认为正确的命题的序号都填上)
15.(理科)抛物线型拱桥的顶点距水面2米时,水面宽8米,若水面上升1米,此时水面宽为
(文科)直线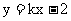 与抛物线
与抛物线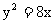 相交于A、B两点,且AB的中点的横坐标为2 ,则k的值为
相交于A、B两点,且AB的中点的横坐标为2 ,则k的值为
14.无论实数b为何值,直线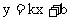 与双曲线
与双曲线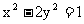 总有公共点,则k的取值范围是
总有公共点,则k的取值范围是
13.椭圆的两焦点为F1(-2,0)、F2(2,0),弦AB过F1 ,且△ABF2的周长为20,则此椭圆方程是
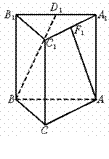
12.如图,A1B1C1-ABC是直三棱柱,∠BCA=90°,点D1、F1分别是A1B1、
A1C1的中点,若BC=CA=CC1,则BD1与AF1所成角的余弦值是( )
A.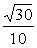 B.
B.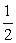 C.
C.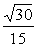 D.
D.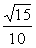
11.已知直线l⊥平面α,直线m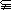 平面β,有下面四个命题:①α∥β
平面β,有下面四个命题:①α∥β l⊥m; ②α⊥β
l⊥m; ②α⊥β l∥m;
l∥m;
 ③l∥m
③l∥m α⊥β;④l⊥m
α⊥β;④l⊥m α∥β 其中正确的两个命题是( )
α∥β 其中正确的两个命题是( )
A.①② B.③④
C.②④ D.①③
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com