
2.(08北京理)已知全集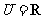 ,集合
,集合 ,
,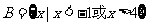 ,那么集合
,那么集合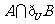 等于( C )
等于( C )
A.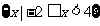 B.
B.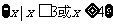
C.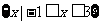 D.
D.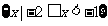
[题型2]抽象集合的运算
[例2](2005全国Ⅰ)设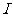 为全集,
为全集,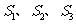 是
是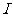 的三个非空子集,且
的三个非空子集,且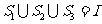 ,
,
则下面论断正确的是 ( C )
A.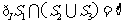 B.
B.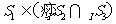
C.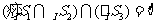 D.
D.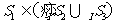
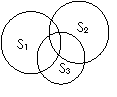 [解析]方法一:特例法 令
[解析]方法一:特例法 令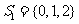 ,
,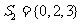 ,
,
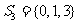 ,则
,则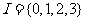 ,检验知C正确.
,检验知C正确.
方法二:利用 图很快得答案C.
图很快得答案C.
[点评] 对抽象集合问题,可以用特例法将它具体化,也可用 图使它直观化,不同的表示方法间可以相互转化;解题时,要善于将集合化成“最简”形式.
图使它直观化,不同的表示方法间可以相互转化;解题时,要善于将集合化成“最简”形式.
[变式与拓展]
1. (2009全国卷Ⅰ理)设集合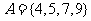 ,
,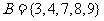 ,全集
,全集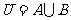 ,则集合
,则集合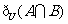 中的元素共有 ( A )
中的元素共有 ( A )
A.3个 B.4个 C.5个 D.6个 
2.集合运算的简单性质:
(1)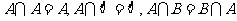 ;
;
(2)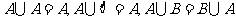 ;
;
(3)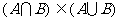 ;
;
(4)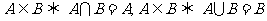 ;
;
(5)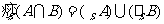 ,
,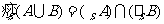 .
.
教材透析
求集合的并、交、补是集合间的基本运算,运算结果仍然是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合 图或数轴进而用集合语言表达,增强数形结合的思想方法.
图或数轴进而用集合语言表达,增强数形结合的思想方法.
典例剖析
[题型1]集合的基本运算
[例1](2009浙江理)设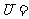
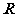 ,
,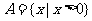 ,
,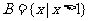 ,则
,则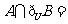 ( )
( )
A.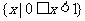 B.
B.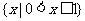 C.
C.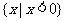 D.
D.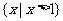
[解析] 对于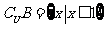 ,因此
,因此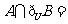
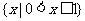 .
.
[点评]本小题主要考查集合运算,集合间的交、补运算是高考中的常考内容,不等式型的补集注意等号,不要出错.
[变式与拓展]
1.集合的基本运算
(1)一般地,由属于集合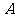 且属于集合
且属于集合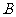 的元素所组成的集合,叫做集合
的元素所组成的集合,叫做集合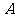 与
与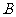 的交集;交集
的交集;交集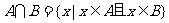 .
.
(2)一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合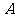 与
与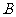 的并集;并集
的并集;并集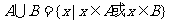 .
.
(3)一般地,如果一个集合包含了我们要研究问题中所涉及的所有元素,那么这个集合称为全集,记作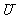 .
.
(4)若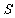 是一个集合,且
是一个集合,且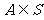 ,则
,则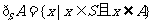 称为集合
称为集合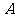 相对于集合
相对于集合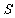 的补集,记作
的补集,记作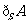 .
.
12.设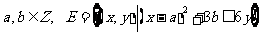 ,点
,点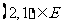 ,但
,但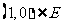 ,
,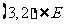 ,求
,求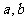 的值.
的值.
[解析]∵点(2,1)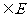 ,∴
,∴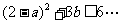 ①
①
∵(1,0)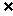 E,(3,2)
E,(3,2)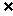 E, ∴
E, ∴ ②
②
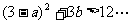 ③
③
由①②得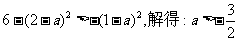 ;
;
类似地由①、③得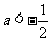 , ∴
, ∴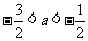 .
.
又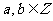 ,∴
,∴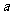 =-1代入①、②得
=-1代入①、②得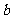 =-1.
=-1.
第二节 集合的运算
自主学习
11.记函数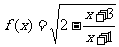 的定义域为
的定义域为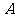 ,
,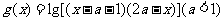 的定义域为B.
的定义域为B.
(1) 求集合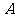 ;
;
(2) 若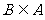 , 求实数
, 求实数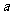 的取值范围.
的取值范围.
[解析](1 )  ,
,
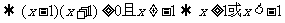 .
.
∴集合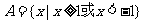 .
.
(2) 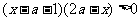 (a<1)
(a<1)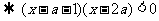 ,
,
∵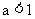 , ∴
, ∴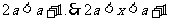 ,
,
∴不等式的解为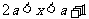 ,
,
∴集合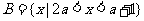 ,
∵
,
∵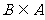 ,
,
∴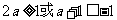 , ∴
, ∴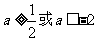 .
.
10.(2008福建)设P是一个数集,且至少含有两个数,若对任意a、b∈P,都有 、
、 、ab、
、ab、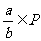 (除数
(除数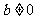 )则称
)则称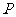 是一个数域,例如有理数集
是一个数域,例如有理数集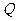 是数域,有下列命题:
是数域,有下列命题:
①数域必含有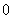 、
、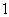 两个数;
两个数;
②整数集是数域;
③若有理数集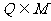 ,则数集
,则数集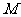 必为数域;
必为数域;
④数域必为无限集.
其中正确的命题的序号是 ①④ (把你认为正确的命题的序号都填上).
9. 设集合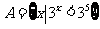 ,
,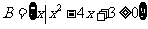 ,则集合
,则集合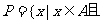
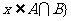
=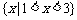 .
.
8. 若集合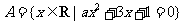 中有且仅有一个元素,则
中有且仅有一个元素,则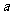 的取值集合是
的取值集合是
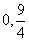 .
.
7.
集合A={x| x2+x-6=0},
B={x| ax+1=0},若B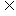 A,则a=
A,则a=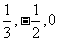 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com