20．(本小题满分13分)

　　　　 已知三点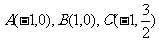，曲线E过C点，且动点P在曲线E上运动，并保持|PA|+|PB|的值不变.

　 (I)求曲线E的方程；

　 (II)若C、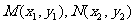是曲线E上的不同三点，直线CM、CN的倾斜角互补.问直线MN的斜率是否是定值？如果是，求出该定值，如果不是，说明理由.

19．(本小题满分12分)

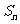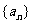已知为数列的前n项和，且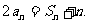

　 (I)若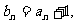证明：数列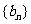是等比数列；

　 (II)求数列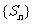的前n项和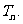

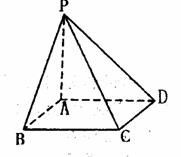
18．(本小题满分12分)

　　 已知四棱锥P-ABCD的侧棱PA⊥平面ABCD，底面ABCD为正方形，且AB=AP=a.

　 (I)若E、F分别是PA、BC的中点，证明EF//平面PCD；

　 (II)求点A到平面PBD的距离.

17．(本小题满分12分)

　　　　 为分析甲、乙两人数学学习状况，学校分别从他两的若干次数学模拟考试中，随机抽取6次的成绩，记录如下：

　 (I)用茎叶图表示这两组数据；

　 (II)现从统计学的角度考虑，你估计哪位学生下次数学考试成绩较高？请说明理由

　 (III)若将频率视为概率，对甲同学在今后的3次数学考试成绩进行预测，求这3次成绩有2次高于80分的概率.

16．(本小题满分12分)

　　　　 在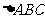中，角A、B、C的对边分别为a、b、c，且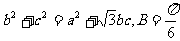，BC边上的中线AM的长为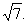

　 (I)求角A、C的大小；

　 (II)求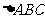的面积.

15．选做题(考生只能从A、B、C题中选作一题)

　　 A、已知直线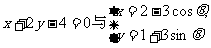(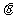为参数)相交于A、B两点，则|AB|=

　　　　 　　　　　　　　　　.

　　 B、若关于x的方程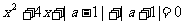有实根，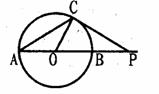

则实数a的取值范围为　　 .　　

C、如图，⊙O的直径AB=6cm，P是延长线上的一点，过

点P作⊙O的切线，切点为C，连结AC，若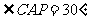

则PC=　　　　 .

14．在区间[0，1]上随机取一个数x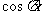，的值介于0到0.5之间的概率为　　　　　　 .

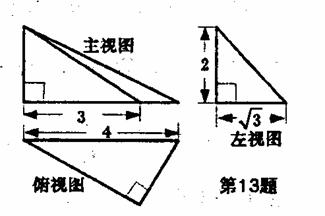
13．一个棱锥的三视图如图，则该棱锥的全面积(单位：cm²)为　　　　 .

12．在中学数学中，从特殊到一般，从具体到抽象是常见的一种思维形式如从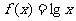可抽象出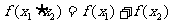的性质，那么由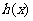=　　　 (填一个具体的函数)可抽象出性质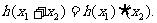

11．调查队想从某学校108名高中生，90名初中生，12名教师中，用分层抽样的方法抽取一个容量为n的样本，要求初中生有6人，则抽取的样本容量n为　　　　 .