
19.(满分14分)(I)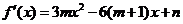 因为
因为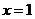 是函数
是函数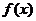 的一个极值点,所以
的一个极值点,所以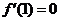 ,即
,即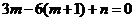 ,所以
,所以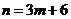
(II)由(I)知,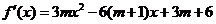 =
=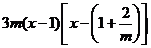
当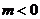 时,有
时,有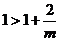 ,当
,当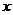 变化时,
变化时,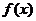 与
与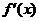 的变化如下表:
的变化如下表:
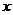 |
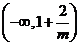 |
 |
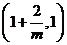 |
1 |
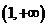 |
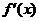 |
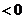 |
0 |
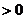 |
0 |
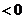 |
|
|
|
|
|
|
|
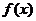 |
调调递减 |
极小值 |
单调递增 |
极大值 |
单调递减 |
故有上表知,当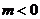 时,
时,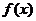 在
在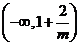 单调递减,在
单调递减,在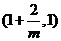 单调递增,在
单调递增,在 上单调递减.
上单调递减.
18.(满分14分).解:该函数为分段函数,第一、二、三级的水价分别为3.7元/t、11.1元/t、
18.5元/t。设用水量为xt,则函数为
(1) 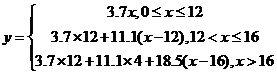 即
即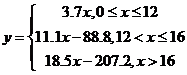 (2)∵
3.7×12=44.4<77.7, ∴ 11.1x-88.8=77.7, ∴ x=15(t)
(2)∵
3.7×12=44.4<77.7, ∴ 11.1x-88.8=77.7, ∴ x=15(t)
17.(满分12分) 设抛物线的方程和为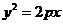 (p>0),则焦点F(
(p>0),则焦点F(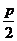 ,0), 通径长为2p
,0), 通径长为2p
由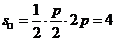 得p=
得p=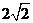
∴所求抛物线的方程为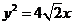
16.(满分12分)(1)∵ f(x)定义域为R且f(x-1)=f(x+1), ∴ f(x+2)=f(x+1+1)=f(x+1-1)=f(x), 则f(x)的一个周期为2,且2n(n∈Z,n≠0)都是y=f(x)的周期。 (2)设1≤x≤2,则-2≤-x≤-1,因此,0≤2-x≤1, 由已知有:f(2-x)=-(2-x)2+4, ∵ f(x)的周期为2,且为偶函数,∴ f(2-x)=f(-x)=f(x). ∴ 当1≤x≤2时,f(x)=-(2-x)2+4。
11.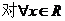 ,
,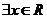 ; 12.
; 12. 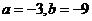 ; 13.
; 13.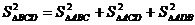 ; 14.
; 14.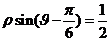 15.
15. 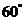 。
。
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
A |
B |
C |
D |
B |
B |
A |
D |
C |
D |
21.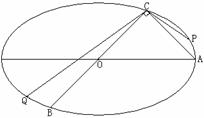 (满分14分)如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且满足
(满分14分)如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且满足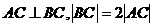 .(1)建立适当的直角坐标系,求椭圆方程; (2)如果P、Q是椭圆上异于A、B的两点,使
.(1)建立适当的直角坐标系,求椭圆方程; (2)如果P、Q是椭圆上异于A、B的两点,使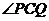 的平分线垂直于OA,求证PQ‖AB.
的平分线垂直于OA,求证PQ‖AB.
广东实验中学2009-2010学年下高二级模块考试
数学(文)解答及说明
20.(满分14分)定义在(0,+∞)上的函数f (x),对于任意的实数m、n∈(0,+∞),都有f(mn)=f(m)+f(n)成立,且当x>1时,f(x)<0.
(1)计算f(1)的值;
(2)证明f(x)在(0,+∞)上是增函数;
(3)比较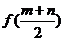 与
与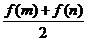 的大小.
的大小.
19.(满分14分)已知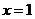 是函数
是函数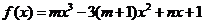 的一个极值点,其中
的一个极值点,其中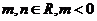 ,
,
(I)求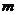 与
与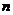 的关系式;(II)求
的关系式;(II)求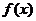 的单调区间;
的单调区间;
18.(满分14分)我国是水资源比较贫乏的国家之一。北方的A市就节水问题,召开了市民听证会,并对“梯级水价”进行激烈讨论,一时成为A市市民的热点话题。“梯级水价”拟定:每户按四人定量,每人每月3t,每t3.7元,12 t内不涨价。第一级为每月12 t内,第二级为12至16 t内,第三级为16 t以上,水价级差拟定按1:3:5进行收费。 (1)请写出水费y与用水量x之间的函数关系式; (2)若某市民家当月水费为77.7元,则当月用水量为多少t?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com