2. 一个容量为n的样本，分成若干组，已知某数的频数和频率分别为50和0.25，则n＝　　　．

1.在用样本频率估计总体分布的过程中，下列说法中正确的是( )

A．总体容量越大，估计越精确　　　　　　　　　　　 B．总体容量越小，估计越精确C．样本容量越大，估计越精确　　　　　　　　　　　 D．样本容量越小，估计越精确

2．　 经典回放：

例1 ：为检测某产品的质量，抽取了一个容量为30的样本，检测结果为一级品5件，二级品8件，三级品13件，次品4件。

⑴ 列出样本的频率分布表；

⑵此种产品为二级品或三级品的概率？

⑶能否画出样本分布的条形图？

分析：当总体中的个体取不同数值很少时，可用频率分布表或频率分布条形图估计总体分布。解：频率分布表如下：

频率分布条形图：

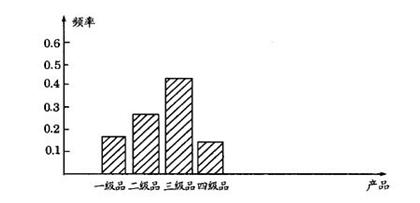
点评：频率分布表中通常有频数、累计频数，频率、累计频率等。其中所有频数的和即样本容量的大小，而所有频率的和恰好为1。

例2：为了了解某地区高三学生的身体发育情况，抽查了地区内100名年龄为17.5岁~18岁的男生的体重情况,结果如下(单位:kg)

试根据上述数据画出样本的频率分布直方图,并对相应的总体分布作出估计

解:按照下列步骤获得样本的频率分布.

(1)求最大值与最小值的差.在上述数据中，最大值是76，最小值是55，它们的差(又称为极差)是76-55=21)所得的差告诉我们，这组数据的变动范围有多大.

(2)确定组距与组数.如果将组距定为2，那么由21÷2=10.5，组数为11，这个组数适合的.于是组距为2，组数为11.

(3)决定分点.根据本例中数据的特点，第1小组的起点可取为54.5，第1小组的终点可取为56.5，为了避免一个数据既是起点，又是终点从而造成重复计算，我们规定分组的区间是“左闭右开”的.这样，所得到的分组是

［54.5，56.5)，［56.5，58.5)，…，［74.5，76.5).

　 (4)列频率分布表,如表①　　　　 频率分布表

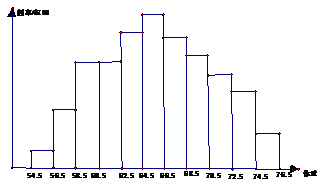(5)绘制频率分布直方图.频率分布直方图如图所示

在得到了样本的频率后，就可以对相应的总体情况作出估计.例如可以估计体重在［64.5，66.5)kg的学生最多，约占学生总数的16%；体重小于58.5kg的学生较少，约占8%；等等

点评：由于图中各小长方形的面积等于相应各组的频率，这个图形的面积反映了数据落在各个小组的频率的大小.在反映样本的频率分布方面，频率分步表比较准确，频率分布直方图比较直观，它们起着相互补充的作用.

[同步训练]

1．　 解析视屏：

(1)　　 频率分布表：当总体很大或不便于获得时，可以用样本的频率分布来估计总体的频率分布。我们把反映总体频率分布的表格为频率分布表。

(2)　　 编制频率分布表的步骤：

① 求全距，决定组数和组距，组距=；

② 分组，区间一般左闭右开(为了遵循统计分组穷尽和互斥原则，所以统计上规定，凡是总体某一个单位的变量值是相邻两组的界限值，这一个单位归入作为下限值的那一组内，即所谓“上限不在内”原则)；

⑶ 登记频数，计算频率，列出频率分布表。

(3)　 条形图：条形图是用宽度相同的条形的高度或长度来表示数据变动的图形。条形图可以横置也可以纵置，纵置时又称为柱形图，也就是说，当各类别放在纵轴时，称为条形图；当各类别放在横轴时，称为柱形图。

(4)　 频率分布直方图：直方图是用矩形的宽度和高度来表示频率分布的图形(在平面直角坐标中，横轴表示数据分组，即各组组距，纵轴表示频率)。

(5)直方图与条形图的不同点：

① 条形图是用条形的长度表示各类别频数的多少，其宽度(表示类别)是固定的；直方图是用面积表示各组频率的多少，矩形的高度表示每一组的频率除以组距，宽度则表示各组的组距，因此其高度与宽度均有意义。

② 此外，由于分组数据具有连续性，直方图的各矩形通常是连续排列，而条形图则是分开排列。

2．　 学法指导：

当总体中的个体取不同数值很少时，可用频率分布表或频率分布条形图估计总体分布；当总体中的个体取不同数值较多，甚至无限时，可用频率分布表或频率分布直方图估计总体分布。

[教师在线]

1．　 学习目标：

体会分布的意义和作用，学会列频率分布表，会画频率分布条形图、直方图，会用频率分布表或分布条形图、直方图估计总体分布，并作出合理解释。在解决问题过程中，进一步体会用样本估计整体的思想，认识统计的实际作用，初步经历收集数据到统计数据的全过程，体会统计思维与确定性思维的差异。

(二)题型

1、配子类型问题

例1：AaBb产生配子种类数：先分解，后组合。(共4种配子：AB、Ab、aB、ab)。

例2：AaBbCc与aaBbCc杂交过程中，配子结合方式：先分解，后组合。(8×4＝32)。

2、子代基因型种类及比例问题

例：AaBBCc×aaBbcc→子代基因型种类及比例：先分解，后组合。(共8种：AaBBCc、AaBBcc、AaBbCc、AaBbcc、aaBBCc、aaBBcc、aaBbCc、aaBbcc，比例相等)。

3、子代表现型及比例问题

例：AaBBCcDd×aaBbCcDD→子代中表现型种类数及A　 B　 C　 D　 在子代中所占比例：先分解，后组合。(子代中表现型种类为：2×1×2×1＝4种，其中A　 B　 C　 D　 在子代中所占比例＝)。

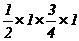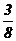[基础训练]

1、不可用2ⁿ表示的是(　 D　 )

A、含有n对基因的个体产生的配子数最多种类

B、含有n对独立遗传的等位基因的个体产生的配子的种类

C、一个DNA分子复制n次后产生的DNA分子数

D、含有n对同源染色体的个体产生的配子种类

2、用纯种的黑色长毛狗与白色短毛狗杂交，F₁全是黑色短毛。F₁的雌雄个体相互交配，F₂的表现型如下表所示。据此可判断控制这两对相对性状的两对基因位于(　 C　 )

A、一对同源染色体上

B、一对姐妹染色单体上

C、两对常染色体上

D、一对常染色体和X染色体上

3、小香猪“天资聪颖”，成为人们的新宠，其背部皮毛颜色是由位于不同常染色体上的两对基因(A、a和B、b)控制的，共有4种表现型：黑色(A　 B　 )、褐色(aaB　 )、棕色(A　 bb)和白色(aabb)。

(1)两只黑色小香猪交配产下一只白色雄性小香猪，则它们再生下一只棕色雌性小香猪的概率是3/32。

(2)现有多对黑色杂合的小香猪，要选育出纯合的棕色小香猪，请简要写出步骤(假设亲本足够多，产生的后代也足够多)。

1从亲本中选择多对雌雄个体进行杂交，得F₁有4种表现型。

2选择F₁中的棕色小香猪与白色小香猪测交，测交后代不出现性状分离的棕色小香猪为纯合子。

[高考模拟]

4、(2007广东高考)某常染色体隐性遗传病在人群中的发病率为1%，色盲在男性中的发病率为7%。现有一对表现正常的夫妇，妻子为该常染色体遗传病致病基因和色盲致病基因携带者。那么他们所生小孩同时患上述两种遗传病的概率是(　 A　 )

A、1/88　　　　　　　　　　 B、1/22　　　　　　　　　　　 C、7/2200　　　　　　　　　 D、3/800

5、(2007湛江模拟)向日葵种子粒大(B)对粒小(b)是显性，含油少(S)对含油多(s)是显性，这两对等位基因按自由组合定律遗传。今有粒大油少和粒小油多的两纯合子杂交，试回答下列问题：

(1)F₂表现型有哪几种？其比例如何？(4种，其表现型及比例为：9粒大油少︰3粒大油多︰3粒小油少︰1粒小油多。)

(2)若获得F₂种子544粒，按理论计算，双显性纯种有多少粒？双隐性纯种有多少粒？粒大油多的有多少粒？(34；34；102。)

(3)怎样才能培育出粒大油多，又能稳定遗传的新品种？并写出简要程序。(自交法。简要程序：第一步：让BBSS与bbss杂交产生F₁：BbSs，第二步：让F₁BbSs自交产生F₂，第三步：选出F₂中粒大油多的个体连续自交，逐代淘汰粒小油多的个体，直到后代不再发生性状分离为止，即获得能稳定遗传的粒大油多的新品种。)

(一)思路：将多对等位基因的自由组合分解为若干个分离定律分别分析，再运用乘法原理将各组情况进行组合。

22．(本题满分10分)

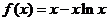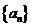设函数．数列满足，．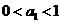

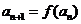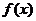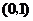(Ⅰ)证明：函数在区间是增函数；

(Ⅱ)证明：；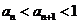

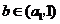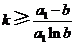(Ⅲ)设，整数．证明：．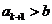

广东实验中学2009-2010学年(下)高二级模块考试