3.已知一个无穷等差数列的首项为a₁,公差为d:

(1)将数列中的前m项去掉，其余各项组成一个新的数列，这个数列是等差数列吗？如果是，它的首项与公差分别是多少？

解：设一无穷等差数列为：a₁,a₂,…,a_m,a_m+1,…,a_n,…

若去掉前m项，则新数列为：a_m+1,…,a_n,…,即首项为a_m+1,公差为d的等差数列.

(2)取出数列中的所有奇数项，组成一个新的数列，这个数列是等差数列吗？如果是，它的首项与公差分别是多少？

解：若设一无穷等差数列为：a₁,a₂,a₃,a₄,a₅,…,a_n,…,则取出数列中的所有奇数项，组成的新数列为：a₁,a₃,a₅,…,a_2m－1,…

即，首项为a₁,公差为2d的等差数列.

(3)取出数列中的所有项数为7的倍数的各项，组成一个新的数列，这个数列是等差数列吗？如果是，它的首项与公差各是多少？

设一无穷等差数列为：a₁,a₂,a₃,…,a_n,…,则新数列为：a₇,a₁₄,a₂₁,…,a_7m,…,即首项为a₇,公差为7d的等差数列.

课本练习

［生］(口答)4.(1)100与180的等差中项为140，(2)－2与6的等差中项为2.

2.等差数列通项公式：a_n=a₁+(n－1)d(n≥1)

推导公式：a_n=a_m+(n－m)d

Ⅱ.讲授新课

［师］首先，请同学们来思考这样一个问题.

(打出投影片

问题1：如果在a与b中间插入一个数A，使a、A、b成等差数列，那么A应满足什么条件？

［生］由等差数列定义及a、A、b成等差数列可得：A－a=b－A,即：A=.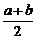

［师］反之，若A=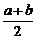,则2A=a+b,A－a=b－A,即a、A、b成等差数列.

总之，A=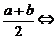a,A,b成等差数列.

也就是说，A=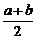是a,A,b成等差数列的充要条件.

如果a、A、b成等差数列，那么A叫做a与b的等差中项.

不难发现，在一个等差数列中，从第2项起，每一项(有穷数列的末项除外)都是它的前一项与后一项的等差中项.

如数列：1，3，5，7，9，11，13，……中，3是1和5的等差中项，5是3和7的等差中项，7是5和9的等差中项等等

进一步思考，同学们是否还发现什么规律呢？

比如5不仅是3和7的等差中项，同时它也是1和9的等差中项，即不仅满足5=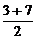，同时还满足5=.

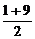再如7不仅是5和9的等差中项，同时它也是3和11的等差中项，还是1和13的等差中项，即：7=.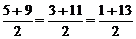

看来，a₂+a₄=a₁+a₅=2a₃,a₄+a₆=a₃+a₇=2a₅

依此类推，可得在一等差数列中，若m+n=p+q,则a_m+a_n=a_p+a_q.

下面，我们来看一个实际问题.(打出投影片)

分析：首先要数学建模，即将实际问题转化为数学问题，然后求其解，最后还要结合实际情况将其还原为实际问题的解.

解：用{a_n}表示梯子自上而下各级宽度所成的等差数列，由已知条件，有

a₁=33,a₁₂=110,n=12.

由通项公式，得a₁₂=a₁+(12－1)d,即：110=33+11d,解得：d=7.

因此，a₂=33+7=40,a₃=40+7=47,a₄=54,a₅=61,a₆=68,a₇=75,a₈=82,a₉=89,a₁₀=96,a₁₁=103.

答案：梯子中间各级的宽度从上到下依次是40 cm,47 cm,54 cm,61 cm,68 cm,75 cm,

82 cm,89 cm,96 cm,103 cm.

评述：要注意将模型的解还原为实际问题的解.

［师］再来看例2.

［生］思考片刻.

［师］分析：由等差数列的定义，要判定{a_n}是不是等差数列，只要看a_n－a_n－1(n≥2)是不是一个与n无关的常数就行了.

解：取数列{a_n}中的任意相邻两项a_n－1与a_n(n≥2)，

a_n－a_n－1=(pn+q)－［p(n－1)+q］

=pn+q－(pn－p+q)=p

它是一个与n无关的常数，所以{a_n}是等差数列，且公差是p.

在通项公式令n=1,得a₁=p+q,所以这个等差数列的首项是p+q,公差是p.看来，等差数列的通项公式可以表示为：a_n=pn+q(其中p、q是常数)

当p=0时，它是一常数数列，从图象上看，表示这个数列的各点均在y=q的图象上.当p≠0时，它是关于n的一次式，从图象上看，表示这个数列的各点均在一次函数y=px+q的图象上.

例如，首项是1，公差是2的无穷等差数列的通项公式为：a_n=2n－1，相应的图象是直线y=2x－1上的均匀排开的无穷多个孤立点.如图所示：

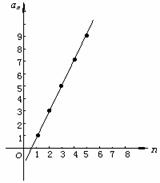
Ⅲ.课堂练习

课本.(师生讨论)

2.在等差数列{a_n}中，若m+n=p+q,则a_m+a_n　　　　　 ap+aq,(填“＞”“=”“＜”)

第二张：记作

［例1］梯子的最高一级宽33 cm，最低一级宽110 cm，中间还有10级，各级的宽度成等差数列，计算中间各级的宽度.

［例2］已知数列的通项公式为a_n=pn+q,其中p、q是常数，且p≠0,那么这个数列是否一定是等差数列？如果是，其首项与公差是什么？

●教学过程

Ⅰ.复习回顾

［师］(提问)：上节课，咱们学习了有关等差数列的哪些内容呢？

［生］(回答)：1.等差数列定义：a_n－a_n－1=d(n≥2)

1.如果在a与b中间插入一个数A，使a、A、b成等差数列，那么A应满足什么条件？

2.提高学生的数学素质.

●教学重点

等差数列的定义、通项公式、性质的理解与应用.

●教学难点

灵活应用等差数列的定义及性质解决一些相关问题.

●教学方法

讲练相结合

结合典型例题，认真分析，讲解，再结合典型习题进行巩固性练习，从而提高分析问题、解决问题的能力.

●教具准备

投影片两张

第一张：记作

1.培养学生的应用意识.

2.进一步熟练掌握等差数列的通项公式及推导公式.

1.明确等差中项的概念.

2.数学建模.

1.等差中项概念.