
读某房屋的冬季、夏季太阳方位示意图,回答4-5题
4.房屋一定坐落在( )
A.东半球

B.西半球 
C.南半球

D.北半球
5.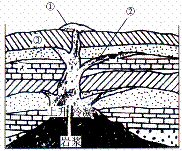 夏至日日出方位为( )
夏至日日出方位为( )
A.①
B.② 
C.③
D.④
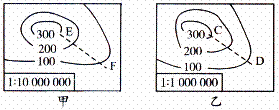
3.读“等高线地形图”,下列叙述正确的是( )

A.甲图反映的范围比乙图小
B.EF处的坡度比CD处大
 C.乙图反映的实际内容更详细
C.乙图反映的实际内容更详细

D.EF间实际距离小于CD

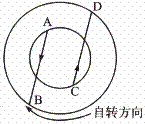
2.读右图(外面箭头表示地球自转方向),下列叙述正确的是( )
A.从A点到B点方向是向西南
B.从C点到D点方向是先东北后东南
C.A到B的方向同C到D的方向相同
D.A到B的方向同C到D的方向正好相反
1.甲地(30°N,160°E)位于乙地(20°N,120°E)的什么方向( )
 A.东北 B.东南
A.东北 B.东南

C.西北 D.西南
21. 成等差数列,
成等差数列,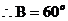 ,
,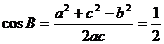 ,
,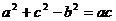
要证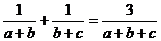 ,只需证
,只需证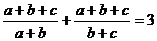 ,
,
只需证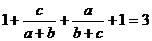 ,只需证
,只需证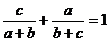 ,
,
只需证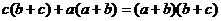 ,即证
,即证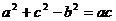 .上式显然成立。得证。
.上式显然成立。得证。

⒘若关于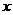 的方程
的方程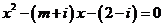 有实数根,求实数
有实数根,求实数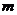 的值.
的值.
⒙假设设备的使用年限x(年)与维修费用y(万元)有如下关系:
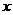 |
2 |
3 |
4 |
5 |
6 |
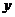 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
(1)求样本中心;
(2)如果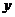 与
与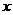 之间具有线性相关关系,求回归直线方程
之间具有线性相关关系,求回归直线方程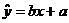 .
.

⒚设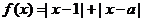 .
.
⑴若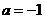 ,解不等式
,解不等式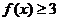 ;⑵若对于任意的
;⑵若对于任意的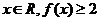 ,求
,求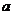 的取值范围.
的取值范围.
⒛已知关于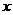 的方程
的方程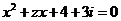 有实数根,求复数
有实数根,求复数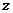 的模
的模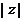 的最小值.
的最小值.
21.若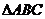 的三内角
的三内角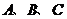 成等差数列,求证:
成等差数列,求证: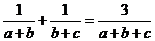 .
.
 参考答案
参考答案
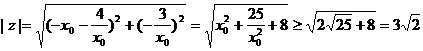 ,
,
当且仅当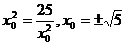 时,等号成立。
时,等号成立。
⒔已知正数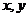 满足
满足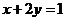 ,则
,则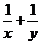 的最小值为______________
的最小值为______________
⒕若不等式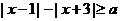 有解,则
有解,则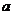 的取值范围为_______________
的取值范围为_______________
⒖若复数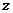 满足
满足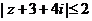 ,则
,则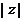 的最小值为_____________
的最小值为_____________
⒗已知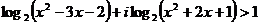 ,则实数
,则实数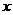 的取值集合为______________
的取值集合为______________
⒈观察数列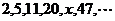 中的
中的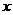 等于( )
等于( )
A.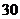 B.
B. 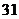 C.
C.
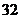 D.
D.
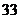
 ⒉在复平面内,复数
⒉在复平面内,复数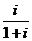 对应的点所在的象限为( )
对应的点所在的象限为( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
⒊否定结论“至多有两个解”的说法中,正确的是( )
A. 有一个解 B. 有两个解 C. 至少有三个解 D. 至少有两个解
⒋下列说法不正确的是( )
A. 流程图通常有一个“起点”,一个或多个“终点”
B. 程序框图是流程图的一种
C. 结构图一般由构成系统的若干要素和表达各要素之间关系的连线(或方向箭头)构成
D. 流程图与结构图是解决同一个问题的两种不同的方法
⒌若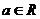 ,且
,且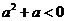 ,则下面式子正确的是( )
,则下面式子正确的是( )
A. 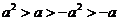 B.
B.
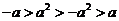
C. 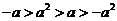 D.
D.
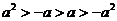
⒍设复数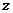 满足
满足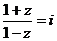 ,则
,则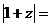 ( )
( )
A. 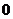 B.
B.
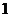 C.
C.
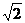 D.
D.
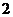
⒎对于推理:若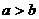 ,则
,则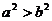 ,因为
,因为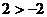 ,则
,则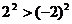 ,即
,即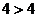 ,下列说法正确的是( )
,下列说法正确的是( )
A. 大前提错误 B. 小前提错误 C. 推理正确 D. 不是演绎推理
⒏线性回归方程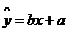 必过定点( )
必过定点( )
A. 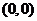 B.
B. 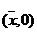 C.
C.
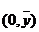 D.
D.
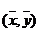
⒐若正数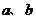 满足
满足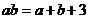 ,则
,则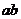 的取值范围为( )
的取值范围为( )
A. 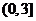 B.
B.
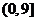 C.
C.
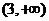 D.
D. 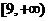
⒑已知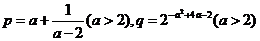 ,则( )
,则( )
A. 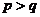 B.
B.
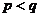 C.
C.
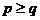 D.
D.
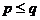
⒒下列说法不正确的是( )
A. 回归分析中,相关指数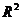 的值越大,说明残差平方和越小
的值越大,说明残差平方和越小
B. 若一组观测值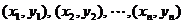 满足
满足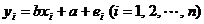 ,若
,若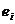 恒为
恒为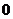 ,则
,则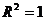
C.回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法
D. 画残差图时,纵坐标为残差,横坐标一定是编号
12. 给出下面类比推理命题(其中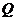 为有理数集,
为有理数集,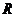 为实数集,
为实数集,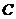 为复数集)
为复数集)
 ⑴“若
⑴“若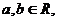 则
则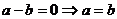 ”类比推出“若
”类比推出“若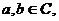 则
则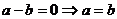 ”
”
 ⑵“若
⑵“若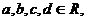 则复数
则复数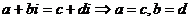 ”类比推出“若
”类比推出“若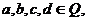 则复数
则复数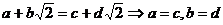 ”
”
⑶“若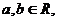 则
则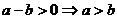 ”类比推出“若
”类比推出“若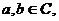 则
则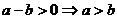 ”
”
其中类比正确的个数为( )
A. 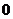 B.
B.
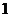 C.
C.
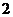 D.
D.
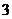
23. 如图,在某城市中,
如图,在某城市中,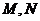 两地之间有整齐的方格形道路网,其中
两地之间有整齐的方格形道路网,其中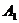 、
、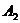 、
、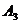 、
、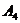 是道路网中位于一条对角线上的4个交汇处.今在道路网
是道路网中位于一条对角线上的4个交汇处.今在道路网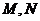 处的甲、乙两人分别要到
处的甲、乙两人分别要到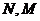 处,他们分别随机地选择一条沿街的最短路径,以相同的速度同时出发,直到到达
处,他们分别随机地选择一条沿街的最短路径,以相同的速度同时出发,直到到达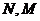 为止.
为止.
(1)求甲经过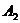 到达N的方法有多少种;
到达N的方法有多少种;
(2)求甲、乙两人在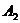 处相遇的概率;
处相遇的概率;
(3)求甲、乙两人相遇的概率.
22.如图,在正方体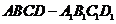 中,
中,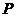 是棱
是棱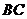 的中点,
的中点,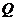 在棱
在棱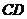 上.
上.
且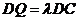 ,若二面角
,若二面角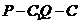 的余弦值为
的余弦值为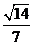 ,求实数
,求实数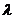 的值.
的值.

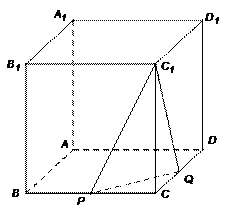
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com