
20.设函数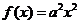 (
(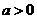 ),
),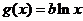 .
.
(1) 若函数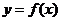 图象上的点到直线
图象上的点到直线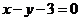 距离的最小值为
距离的最小值为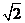 ,求
,求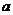 的值;
的值;
(2) 关于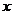 的不等式
的不等式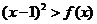 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数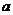 的取值范围;
的取值范围;
(3) 对于函数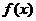 与
与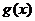 定义域上的任意实数
定义域上的任意实数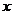 ,若存在常数
,若存在常数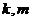 ,使得
,使得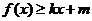 和
和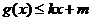 都成立,则称直线
都成立,则称直线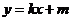 为函数
为函数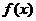 与
与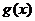 的“分界线”.设
的“分界线”.设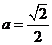 ,
,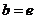 ,试探究
,试探究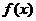 与
与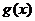 是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
附加题部分
A.选修4-1(几何证明选讲)
如图,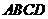 是边长为
是边长为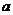 的正方形,以
的正方形,以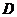 为圆心,
为圆心,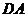 为半径的圆弧与以
为半径的圆弧与以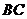 为直径的
为直径的 交于点
交于点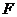 ,延长
,延长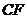 交
交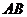 于
于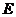 .(1)求证:
.(1)求证: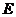 是
是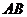 的中点;(2)求线段
的中点;(2)求线段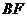 的长.
的长.
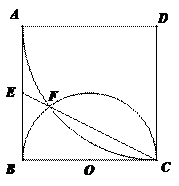
B.选修4-2(矩阵与变换)
已知矩阵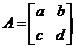 ,若矩阵
,若矩阵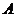 属于特征值3的一个特征向量为
属于特征值3的一个特征向量为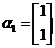 ,属于特征值-1的一个特征向量为
,属于特征值-1的一个特征向量为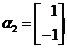 ,求矩阵
,求矩阵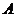 .
.
C.选修4-4(坐标系与参数方程)
在极坐标系中,曲线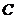 的极坐标方程为
的极坐标方程为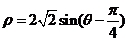 ,以极点为原点,极轴为
,以极点为原点,极轴为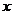 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线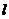 的参数方程为
的参数方程为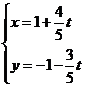 (
(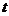 为参数),求直线
为参数),求直线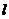 被曲线
被曲线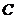 所截得的弦长.
所截得的弦长.
D.选修4-5(不等式选讲)
已知实数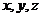 满足
满足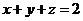 ,求
,求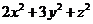 的最小值;
的最小值;
19.某单位有员工1000名,平均每人每年创造利润10万元。为了增加企业竞争力,决定优化产业结构,调整出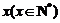 名员工从事第三产业,调整后他们平均每人每年创造利润为
名员工从事第三产业,调整后他们平均每人每年创造利润为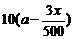 万元
万元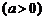 ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高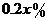 .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)在(1)的条件下,若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,则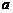 的取值范围是多少?
的取值范围是多少?
(3)设调出的员工创造的年总利润的最大值为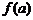 ,在(1)的条件下,试写出
,在(1)的条件下,试写出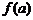 的表达式(直接写出结果,不需要给出演算步骤)。
的表达式(直接写出结果,不需要给出演算步骤)。
18.已知数列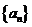 是各项均不为0的等差数列,
是各项均不为0的等差数列,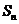 为其
为其 前
前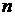 项和,且满足
项和,且满足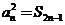 ,令
,令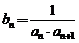 ,数列
,数列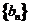 的前n项和为
的前n项和为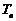 .
.
(1)求数列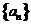 的通项公式及数列
的通项公式及数列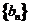 的前n项和为
的前n项和为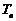 ;
;
(2)是否存在正整数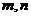
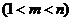 ,使得
,使得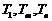 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的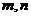
 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
17.已知圆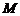 的方程为
的方程为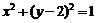 ,直线
,直线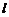 的方程为
的方程为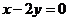 ,点
,点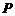 在直线
在直线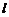 上,过
上,过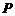 点作圆
点作圆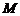 的切线
的切线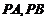 ,切点为
,切点为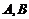 .
.
(1)若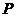 点的坐标为
点的坐标为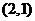 ,过
,过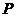 作直线与圆
作直线与圆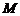 交于
交于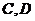 两点,当
两点,当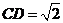 时,求直线
时,求直线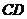 的方程;
的方程;
(2)求证:经过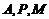 三点的圆必过定点,并求出所有定点的坐标.
三点的圆必过定点,并求出所有定点的坐标.
16.如图,平面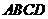
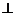 平面
平面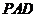 ,△
,△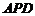 是直角三角形,
是直角三角形,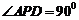 ,四边形
,四边形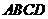 是直角梯形,其中
是直角梯形,其中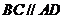 ,
,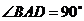 ,
,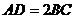 ,
,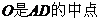
(1)求证: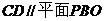 ;
;
 (2)求证:
(2)求证: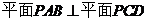 .
.
15.在三角形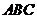 中,已知
中,已知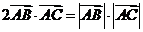 ,设
,设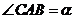 ,
,
(1)求角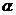 的值;
的值;
(2)若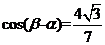 ,其中
,其中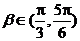 ,求
,求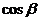 的值.
的值.
14.设函数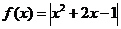 ,若
,若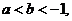 且
且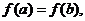 则
则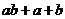 的取值范围为 .
的取值范围为 .
13.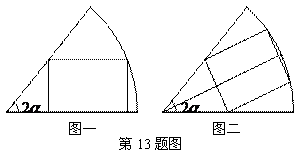 已知扇形的圆心角为
已知扇形的圆心角为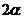 (定值),半径为
(定值),半径为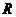 (定值),分别按图一、二作扇形的内接矩形,若按图一作出的矩形面积的最大值为
(定值),分别按图一、二作扇形的内接矩形,若按图一作出的矩形面积的最大值为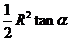 ,则按图二作出的矩形面积的最大值为
.
,则按图二作出的矩形面积的最大值为
.
12.已知椭圆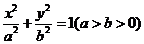 的离心率是
的离心率是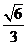 ,过椭圆上一点
,过椭圆上一点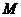 作直线
作直线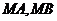 交椭圆于
交椭圆于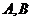 两点,且斜率分别为
两点,且斜率分别为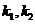 ,若点
,若点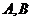 关于原点对称,则
关于原点对称,则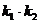 的值为
.
的值为
.
11.在数列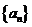 中,若对任意的
中,若对任意的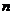 均有
均有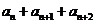 为定值(
为定值(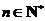 ),且
),且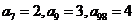 ,则此数列
,则此数列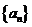 的前100项的和
的前100项的和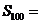 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com