
24.(本小题满分10分)选修4-5:不等式选讲
设函数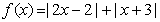 .
.
(Ⅰ)解不等式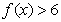 ;
;
(Ⅱ)若关于 的不等式
的不等式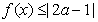 的解集不是空集,试求
的解集不是空集,试求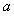 的取值范围.
的取值范围.
23.(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线C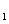 :
: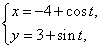 (t为参数), C
(t为参数), C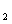 :
: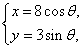 (
(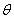 为参数)。
为参数)。
(Ⅰ)化C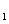 ,C
,C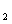 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)若C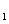 上的点P对应的参数为
上的点P对应的参数为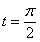 ,Q为C
,Q为C 上的动点,求PQ中点M到直线
上的动点,求PQ中点M到直线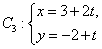 (t为参数)距离的最小值。
(t为参数)距离的最小值。
22.(本小题满分10分)选修4-1:几何证明选讲
如图,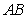 是⊙
是⊙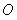 的直径,
的直径,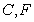 是⊙
是⊙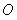 上的点,
上的点,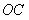 垂直于直径
垂直于直径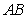 ,
,
过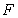 点作⊙
点作⊙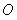 的切线交
的切线交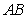 的延长线于
的延长线于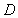 .连结
.连结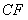 交
交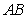 于
于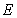 点.
点.
(Ⅰ)求证: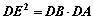 ;
;
(Ⅱ)若⊙ 的半径为
的半径为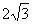 ,
,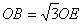 ,求
,求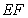 的长.
的长.

21.(本小题满分12分)
如图,椭圆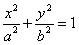 上的点
上的点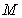 与椭圆右焦点
与椭圆右焦点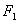 的连线
的连线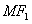 与x轴垂直,且
与x轴垂直,且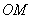 (
(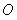 是坐标原点)与椭圆长轴和短轴端点的连线
是坐标原点)与椭圆长轴和短轴端点的连线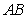 平行.
平行.
(Ⅰ)求椭圆的离心率;
(Ⅱ)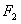 是椭圆的左焦点,
是椭圆的左焦点,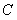 是椭圆上的任一点,
是椭圆上的任一点,
证明: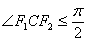
(Ⅲ)过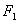 且与
且与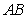 垂直的直线交椭圆于
垂直的直线交椭圆于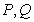 ,若
,若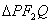 的面积是
的面积是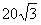 , 求此时椭圆标准方程
, 求此时椭圆标准方程
请考生在第22,23,24三题中任选一题做答,如果多做,则按所做的第一题计分。
20.(本小题满分12分)
已知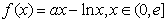 ,
,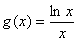 ,其中
,其中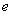 是自然对数的底数,
是自然对数的底数,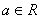 。
。
(Ⅰ)当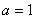 时, 求
时, 求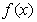 的单调区间且证明不等式
的单调区间且证明不等式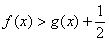 ;
;
(Ⅱ)是否存在实数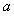 ,使
,使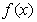 的最小值是3,若存在,求出
的最小值是3,若存在,求出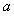 的值;若不存在,说明理由.
的值;若不存在,说明理由.
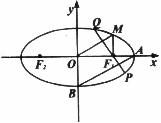
19.(本小题满分12分)
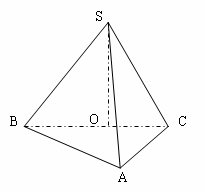
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,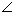 BAC=90o,O为BC的中点。
BAC=90o,O为BC的中点。
(Ⅰ)求证:SO⊥平面ABC;
(Ⅱ)求二面角A-SC-B的余弦值.







18.(本小题满分12分)
在10件产品中,有3件一等品,4件二等品,3件三等品。从这10件产品中任取3件,求:
(I) 取出的3件产品中一等品件数X的分布列和数学期望; 
(II)取出的3件产品中一等品件数多于二等品件数的概率。 
17. (本小题满分12分)
在 中,
中,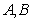 为锐角,角
为锐角,角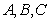 所对应的边分别为
所对应的边分别为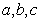 ,且
,且
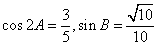

(I)求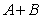 的值;
的值; 
(II)若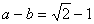 ,求
,求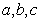 的值。
的值。





16.给出下列命题:
(1)在△ABC中,若A<B,则sinA<sinB;
(2)将函数y=sin(2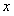 +
+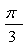 )图象向右平移
)图象向右平移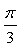 个单位,得到函数y=sin2
个单位,得到函数y=sin2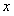 的 图象;
的 图象; 
(3)在△ABC中, 若AB=2,AC=3,∠ABC=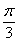 ,则△ABC必为锐角三角形;
,则△ABC必为锐角三角形;
(4)在同一坐标系中,函数y=sin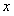 的图象和函数y=
的图象和函数y=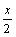 的图象有三个公共点;
的图象有三个公共点;
其中正确命题的序号是
(写出所有正确命题的序号)。
15.将一颗骰子连续抛掷三次,它落地时向上的点数依次成为等差数列的概 率为__________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com