3、从《木兰诗》中“爷”的称呼看中国古代的称呼与地位

2、从《木兰诗》中看中国古代女子的服饰

第二课时

一主动发现问题，寻找探究点

问题(包括老师提出的启发性问题)展开讨论，讨论的形式可以灵活多样。

探究点参考备案：

1、南朝民歌的修辞运用(或特点)

3.　 O为三角形ABC内一点，若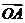++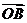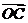=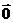，则O是三角形ABC的(　 )。

A．内心　 B．外心　 C．垂心　 D．重心

2．在四边形ABCD中，+++=　　　　　 。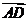

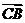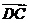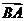1．向量a表示“向东走2km”，向量b表示“向南走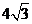km”，则a+b+a表示　　　　　 。

1°向量加法的几何法则

　　　　　 2°换律和结合律

　　　　　 3°注意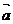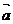：|+| > || + ||不一定成立，因为共线向量不然。

问题1：a+b的方向与a，b的方向有何关系？

︱　　 a+b︱与︱a︱，︱b︱有何关系？

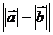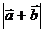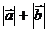问题2：讨论：、和的大小关系

6.向量加法的多边形法则

问题2：如何求平面内n(n＞3)个向量的和向量？

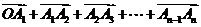
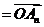
问题3：若点O与点An重合，你将得出什么结论？

例1：如图，一艘船从A点出发以2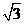　 km/h的速度向垂直于对岸的方向行驶，同时河水的流速为2km/h。求船实际航行速度的大小与方向(用与水流方向的夹角表示)。

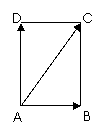
例2：某人先位移向量a:“向东走3km”，接着再位移向量b：“向北走3km”，求a+b

4．加法的交换律和平行四边形法则

上题中+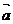的结果与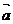+是否相同？

　 从而得到：1°向量加法的平行四边形法则

　　 2°向量加法的交换律：+=+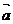

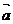
问题1：两种求和法则有什么关系？

向量加法的三角形法则与平行四边形法则是一致的，但两个向量共线时，三角形法则更有优势。

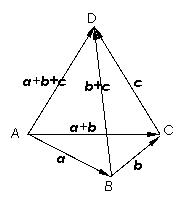加法的结合律：(+) +=+ (+)

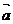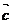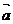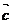证：如图：

从而，多个向量的加法运算可以按照任意的次序、任意的组合来进行。