
8.质点从A到B沿直线运动,已知初速度为零,从A到中间某一点C的加速度为a1,方向与运动方向相同,从C到B的加速度大小为a2,方向与运动方向相反,到达B的速度恰好为零,AB=L,下列说法正确的是( )
A.A到B的平均速度
B.A到B的平均速度
C.过C点的瞬时速度
D.SAC∶SCB =a2∶a1
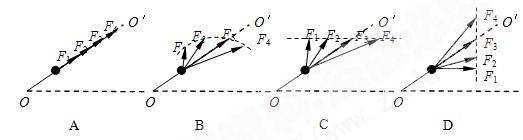
7.如图所示,小车上固定着硬杆,杆的端点固定着一个质量为m的小球.当小车有水平向右的加速度且逐渐增大时,杆对小球的作用力的变化(用F1至F4变化表示)可能是下图中的( 沿杆方向)( )
沿杆方向)( )
6.如图所示,物体P、Q恰好静止,不计摩擦及绳和滑轮的重力,将滑轮B向右移动时,滑轮A将 ( )
A. 上升 B. 不动
C. 下降 D. 无法判断
5.如图是给墙壁粉刷涂料用的“涂料滚”的示意图.使用时,用撑竿推着粘有涂料的涂料滚沿墙壁上下缓缓滚动,把涂料均匀地粉刷到墙上.撑竿的重量和墙壁的摩擦均不计,而且撑竿足够长,粉刷工人站在离墙壁一定距离处缓缓上推涂料滚,该过程中撑竿对涂料滚的推力为F1,涂料滚对墙壁的压力为F2,以下说法正确的是( )
A.F1增大 , F2减小 B.F1减小, F2 增大
C.F1、、F2均增大 D.F1、、F2均减小


4.三个力,一个是12N,一个是5N,一个是8N,那么这三个力的合力的说法正确的是( )
A.合力的最小值是1N B.合力的最小值是0
C.合力不可能是20N D.合力不可能是30N
3.某人从楼顶由静止释放一颗石子,如果忽略空气对石子的阻力,利用下面的哪些已知量可以测量这栋楼的高度H (已知重力加速度为g)( )
A.石子落地时的速度
B.石子下落的时间
C.石子下落最初ls内的位移
D.石子下落最后1s内的位移
2、春天有许多游客放风筝,会放风筝的人,可使风筝静止在空中,以下四幅图中AB代表风筝截面,OL代表风筝线,风向水平,风筝可能静止的是( )
1、关于摩擦力,以下说法正确的是( )
A.两物体接触面间有摩擦,则一定有弹力存在
B.摩擦力大小与接触面间的弹力大小成正比
C.摩擦力的方向与物体运动方向一定相反
D.摩擦力的方向与接触面间的弹力方向一定垂直
[例1] 设函数 满足
满足 ,且
,且 (
( )=0,
)=0, 、
、 ∈R;求证:
∈R;求证: 为周期函数,并指出它的一个周期。
为周期函数,并指出它的一个周期。
分析与简证:由
想: =2cos
=2cos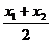 cos
cos
原型: =
=
 ,为周期函数且2π为它的一个周期。
,为周期函数且2π为它的一个周期。
猜测: 为周期函数,2π为它的一个周期
为周期函数,2π为它的一个周期
令 =
= +
+ ,
,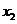 =
= 则
则 =0
=0
∴
∴ 为周期函数且2π是它的一个周期。
为周期函数且2π是它的一个周期。
[例2] 已知函数 满足
满足 ,若
,若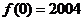 ,试求
,试求 (2005)。
(2005)。
分析与略解:由
想: (
( +
+ )=
)=
原型: =
=
 为周期函数且周期为4×
为周期函数且周期为4× =π。
=π。
猜测: 为周期函数且周期为4×1=4
为周期函数且周期为4×1=4
∵ =
=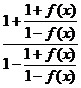 =-
=-
∴
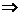
 (
( +4)=
+4)=
∴ 是以4为周期的周期函数
是以4为周期的周期函数
又∵f(2)=2004
∴ =
= =
= =-
=-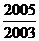
∴f(2005)=-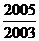
[例3] 已知函数 对于任意实数
对于任意实数 、
、 都有
都有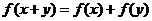 ,且当
,且当 >0时,
>0时, >0,
>0, (-1)=-2,求函数
(-1)=-2,求函数 在区间[-2,1]上的值域。
在区间[-2,1]上的值域。
分析与略解:由: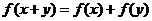
想: (
( +
+ )=
)=
 +
+

原型: =
=
 (
( 为常数)为奇函数。
为常数)为奇函数。 <0时为减函数,
<0时为减函数, >0时为增函数。
>0时为增函数。
猜测: 为奇函数且
为奇函数且 为R上的单调增函数,且
为R上的单调增函数,且 在[-2,1]上有
在[-2,1]上有 ∈[-4,2]
∈[-4,2]
设 <
<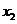 且
且 ,
,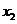 ∈R 则
∈R 则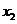 -
- >0 ∴
>0 ∴ (
(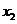 -
- )>0
)>0
∴
=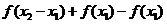 =
= >0
>0
∴ ,∴
,∴ 为R上的单调增函数。
为R上的单调增函数。
令 =
= =0,则
=0,则 (0)=0,令
(0)=0,令 =-
=- ,则
,则 (-
(- )=-
)=-
∴ 为R上的奇函数。
为R上的奇函数。
∴ (-1)=-
(-1)=-  (1)=-2 ∴
(1)=-2 ∴ (1)=2,
(1)=2, (-2)=2
(-2)=2 (-1)=-4
(-1)=-4
∴-4≤ ≤2(x∈[-2,1])
≤2(x∈[-2,1])
故 在[-2,1]上的值域为[-4,2]
在[-2,1]上的值域为[-4,2]
[例4] 已知函数 对于一切实数
对于一切实数 、
、 满足
满足 (0)≠0,
(0)≠0, ,且当
,且当 <0时,
<0时, >1
>1
(1)当 >0时,求
>0时,求 的取值范围
的取值范围
(2)判断 在R上的单调性
在R上的单调性
分析与略解:由:
想:
原型: =
=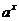 (
(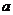 >0,
>0, 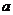 ≠1),
≠1), =1≠0。当
=1≠0。当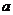 >1时为单调增函数,且
>1时为单调增函数,且 >0时,
>0时, >1,
>1, <0时,0<
<0时,0< <1;0<
<1;0<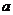 <1时为单调减函数,且
<1时为单调减函数,且 <0时,
<0时, >1,
>1, >0时,0<
>0时,0< <1。
<1。
猜测:  为减函数,且当
为减函数,且当 >0时,0<
>0时,0< <1。
<1。
(1)对于一切 、
、 ∈R,
∈R, 且
且 (0)≠0
(0)≠0
令 =
= =0,则
=0,则 (0)=1,现设
(0)=1,现设 >0,则-
>0,则- <0,∴f(-
<0,∴f(- ) >1
) >1
又 (0)=
(0)= (
( -
- )=
)= 
 =1
∴
=1
∴ =
= >1
>1
∴0< <1
<1
(2)设 <
<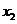 ,
, 、
、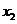 ∈R,则
∈R,则 -
-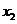 <0,
<0, (
( -
-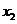 )>1且
)>1且
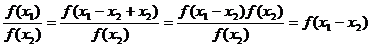 >1
>1
∴ ,
∴f(x)在R上为单调减函数
,
∴f(x)在R上为单调减函数
[例5] 已知函数 定义域为(0,+∞)且单调递增,满足
定义域为(0,+∞)且单调递增,满足 (4)=1,
(4)=1,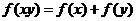
(1)证明: (1)=0;(2)求
(1)=0;(2)求 (16);(3)若
(16);(3)若 +
+  (
( -3)≤1,求
-3)≤1,求 的范围;
的范围;
(4)试证 (
( )=
)=
 (n∈N)
(n∈N)
分析与略解:由: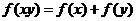
想: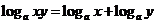 (
( 、
、 ∈R+)
∈R+)
原型: (
(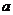 >0,
>0,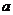 ≠0)
≠0)
猜测: 有
有 (1)=0,
(1)=0, (16)=2,……
(16)=2,……
(1)令 =1,
=1, =4,则
=4,则 (4)=
(4)= (1×4)=
(1×4)= (1)+
(1)+ (4)∴
(4)∴ (1)=0
(1)=0
(2) (16)=
(16)= (4×4)=
(4×4)= (4)+
(4)+ (4)=2
(4)=2
(3) +
+ (
( -3)=
-3)= [
[ (
( -3)]≤1=
-3)]≤1= (4)
(4)
 在(0,+∞)上单调递增
在(0,+∞)上单调递增
∴ 
∴  ∈(3,4]
∈(3,4]
(4)∵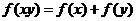
∴
[例6] 已知函数 对于一切正实数
对于一切正实数 、
、 都有
都有 且
且 >1时,
>1时, <1,
<1, (2)=
(2)=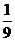
(1)求证: >0;(2)求证:
>0;(2)求证:
(3)求证: 在(0,+∞)上为单调减函数
在(0,+∞)上为单调减函数
(4)若 =9,试求
=9,试求 的值。
的值。
分析与简证:由 ,
,
想:
原型: (
( 为常数(
为常数( =
= )
)
猜测: >0,在(0,+∞)上为单调减函数,……
>0,在(0,+∞)上为单调减函数,……
(1)对任意 >0,
>0, =
= )=
)= ≥0
≥0
假设存在 >0,使
>0,使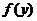 =0,则对任意
=0,则对任意 >0
>0
 =f(
=f(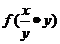 =
= =0,这与已知矛盾
=0,这与已知矛盾
故对任意 >0,均有
>0,均有 >0
>0
(2)∵ ,
, >0, ∴
>0, ∴ (1)=1
(1)=1
∴
 (
( )=
)= (
( ·
· )=
)= (1)=1 ∴
(1)=1 ∴
(3) 、
、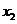 ∈(0,+∞),且
∈(0,+∞),且 <
<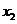 ,则
,则 >1,∴
>1,∴ (
( )<1,
)<1,
∴ 即
即
∴ 在(0,+∞)上为单调减函数。
在(0,+∞)上为单调减函数。
(4)∵ (2)=
(2)=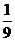 ,
, (
( )=9
∴
)=9
∴ (2)
(2) (
( )=1
)=1
∴ (2
(2 )=1=f(1),而
)=1=f(1),而 在(0,+∞)是单调减函数
在(0,+∞)是单调减函数
∴2 =1
即
=1
即 =
=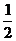
综上所述,由抽象函数问题的结构特征,联想已学过的具有相同或相似结构的基本(原型)函数,并由基本函数的相关结构,预测、猜想抽象函数可能具有的性质 “抽象--具体--抽象”的“原型”联想思维方式,可使抽象函数问题顺利获解,且进一步说明,学生学好大纲规定的几种基本函数相关知识的重要性。
6、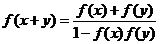 --
-- =
=

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com