
2.用反证法证明:“ ”,应假设为( ).
”,应假设为( ).
A. B.
B. C.
C. D.
D.
1.下列各数中: ,
, ,
, ,
, ,
, ,
, ,,纯虚数的个数有(
)个
,,纯虚数的个数有(
)个
A.0个 B.1个 C.2个 D.3个
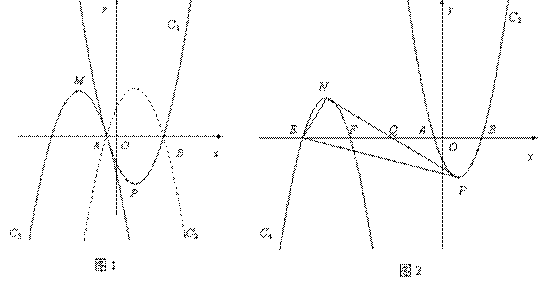
24.如图,已知抛物线C1: 的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点A的横坐标是
的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点A的横坐标是 .
.
(1)求 点坐标及
点坐标及 的值;
的值;
(2)如图(1),抛物线C2与抛物线C1关于x轴对称,将抛物线C2向左平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点A成中心对称时,求C3的解析式 ;
;
(3)如图(2),点Q是x轴负半轴上一动点,将抛物线C1绕点Q旋转180°后得到抛物线C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、E为顶点的三角形是直角三角形时,求顶点N的坐标.

25.已知,正方形ABCD中,∠MAN=45°, ∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.
(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数
量关系: ;
(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由.如果成立请证明;
(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.
(可利用(2)得到的结论)
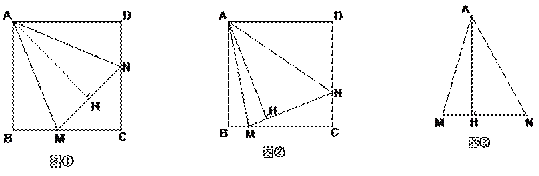
平谷区2009-2010学年度第二学期初三第一次统一练习
23.已知:关于 的一元二次方程
的一元二次方程 (m为实数)
(m为实数)
(1)若方程有两个不相等的实数根,求 的取值范围;
的取值范围;
(2)在(1)的条件下,求证:无论 取何值,抛物线
取何值,抛物线 总过
总过 轴上的一个固定点;
轴上的一个固定点;
(3)若 是整数,且关于
是整数,且关于 的一元二次方程
的一元二次方程 有两个不相等的整数根,把抛物线
有两个不相等的整数根,把抛物线 向右平移3个单位长度,求平移后的解析式.
向右平移3个单位长度,求平移后的解析式.
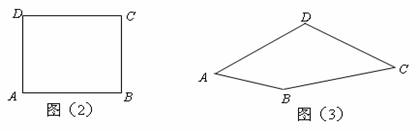
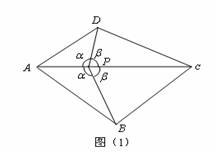
22.如图(1),凸四边形 ,如果点
,如果点 满足
满足
 ,且
,且 ,
,
则称点 为四边形
为四边形 的一个半等角点.
的一个半等角点.
(1)在图(2)正方形 内画一个半等角点
内画一个半等角点 ,且满足
,且满足 ;
;
(2)在图(3)四边形 中画出一个半等角点
中画出一个半等角点 ,
,
保留画图痕迹(不需写出画法).
21.解应用题:
某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
|
类型 价格 |
A型 |
B型 |
|
进价(元/盏) |
40 |
65 |
|
标价(元/盏) |
60 |
100 |
(1)这两种台灯各购进多少盏?
 (2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏 ?
(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏 ?
20.初中生对待学习的态度一直是教育工作者关注的问题之一.
为此,某区教委对该区部分学校的八年级学生对待学习的态度
进行了一次抽样调查(把学习态度分为三个层级,A级:对学
习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴
趣),并将调查结果绘制成图①和图②的统计图(不完整).
请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计该区近20000名初中生中大
约有多少名学生学习态度达标(达标包括A级和B级)?
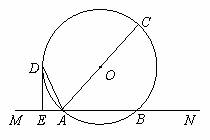
19. 已知,如图,直线MN交⊙O于A,B两点,AC是直径,
AD平分 CAM交⊙O于D,过D作DE⊥MN于E.
CAM交⊙O于D,过D作DE⊥MN于E.
(1)求证:DE是⊙O的切线;
(2)若 cm,
cm, cm,求⊙O的半径.
cm,求⊙O的半径.
18.如图,有一块半圆形钢板,直径AB=20cm,计划将此钢板切割成下底为AB的等腰梯形,上底CD的端点在圆周上,且CD=10cm.求图中阴影部分的面积.
17.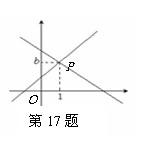 如图,直线
如图,直线 :
: 与直线
与直线 :
: 相交于点
相交于点 .
.
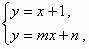 (1)求
(1)求 的值;
的值;
(2)不解关于 的方程组
请你直接写出它的解;
的方程组
请你直接写出它的解;
(3)直线 :
: 是否也经过点
是否也经过点 ?请说明理由.
?请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com