
19.
18.
22.(本小题满分12分)已知数列{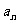 }满足
}满足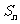 =
=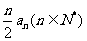 ,
,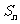 是{
是{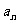 }的前
}的前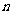 项的和,
项的和,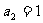 . (1)求
. (1)求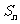 ;(2)证明:
;(2)证明: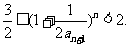
太 原 五 中
2009-2010学年度第二学期月考试题(五月)
高三数学答卷纸
21. (本小题满分12分) 已知两定点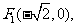
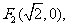 满足条件
满足条件 的点
的点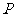 的轨迹是曲线
的轨迹是曲线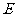 ,直线
,直线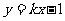 与曲线
与曲线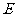 交于
交于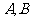 两点 如果
两点 如果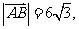 且曲线
且曲线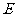 上存在点
上存在点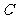 ,使
,使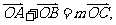 求
求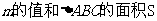
17 (本小题满分10分) 已知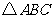 的面积为
的面积为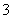 ,且满足
,且满足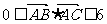 ,设
,设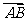 和
和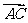 的夹角为
的夹角为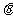
(I)求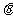 的取值范围;
的取值范围;
(II)求函数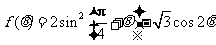 的最大值与最小值
的最大值与最小值
18.
(本小题满分12分) 甲、乙、丙三人按下面的规则进行乒乓球比赛: 第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为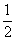 ,且各局胜负相互独立.
,且各局胜负相互独立.
求:(I)打满3局比赛还未停止的概率;
(II)比赛停止时已打局数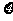 的分别列与期望E
的分别列与期望E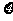 .
.
19(本小题满分12分) 已知定义在正实数集上的函数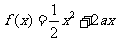 ,
,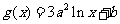 ,其中
,其中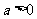 设两曲线
设两曲线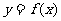 ,
,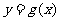 有公共点,且在该点处的切线相同
有公共点,且在该点处的切线相同
(I)用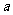 表示
表示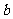 ,并求
,并求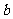 的最大值;
的最大值;
(II)求证: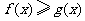 (
(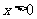 )
)
20
(本小题满分12分)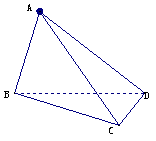 如图,在三棱锥A-BCD中,侧面ABD、 ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、 ACD是全等的直角三角形,AD是公共的斜边,且AD=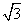 ,BD=CD=1,另一个侧面是正三角形.
,BD=CD=1,另一个侧面是正三角形.
(1) 求证:AD^BC;
(2) 求二面角B-AC-D的大小;
(3) 在直线AC上是否存在一点E,使ED与面BCD成30°角?若存在,确定E的位置;若不存在,说明理由
16.给出下列四个命题:
①动点M到两定点A、B的距离之比为常数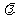
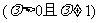 ,则动点M的轨迹是圆;
,则动点M的轨迹是圆;
②椭圆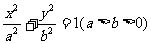 的离心率为
的离心率为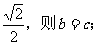
③双曲线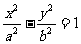
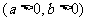 的焦点到渐近线的距离是
的焦点到渐近线的距离是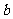 ;
;
④已知抛物线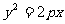 上两点
上两点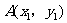 ,
, 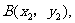 且
且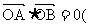
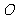 为原点),则
为原点),则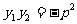 .
.
其中的真命题是_____________.(把你认为是真命题的序号都填上)
15.将10个相同的小球装入编号为1、2、3的三个盒子中(每次要把10个小球装完),要求每个盒子里小球的个数不小于盒子的编号数,这样的装法共有_________种.(要求用数字作答)
14. 在数列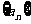 ,如果存在非零实数
,如果存在非零实数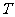 使得
使得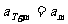 对于任意的正整数
对于任意的正整数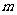 均成立,那么称
均成立,那么称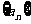 为周期数列,其中
为周期数列,其中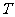 叫周期,已知周期数列
叫周期,已知周期数列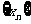 满足
满足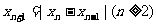 ,如果
,如果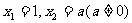 ,当数列
,当数列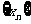 的周期最小时,数列
的周期最小时,数列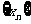 的前2010项的和是________.
的前2010项的和是________.
13. 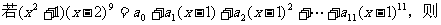
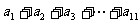 的值为 _______ .
的值为 _______ .
12.已知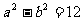 ,则
,则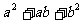 的最小值为 ( )
的最小值为 ( )
(A)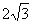 (B)
(B)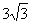 (C)
(C)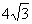 (D)
(D)
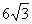
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com