
3.单元Ⅱ中复习的重点是匀变速直线运动规律的应用,本章中的题目常可一题多解,且各种解法有时繁简程度差别很大,应要求学生记住由匀变速直线运动的基本公式推出的一些推论,并训练学生熟练地运用它们来解题.
2.平均速度的概念及公式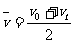 是处理运动学问题常用到的知识点,且在实用中常可发挥独到的作用.但若不注意理解概念的意义和公式的适用条件,也常可造成乱套公式的错误.建议结合例题和单元练习中的有关题目,进一步强调理解物理概念和把握物理规律和公式适用条件的重要性.
是处理运动学问题常用到的知识点,且在实用中常可发挥独到的作用.但若不注意理解概念的意义和公式的适用条件,也常可造成乱套公式的错误.建议结合例题和单元练习中的有关题目,进一步强调理解物理概念和把握物理规律和公式适用条件的重要性.
1.加速度的概念及运动图象是第Ⅰ单元的复习重点和难点,通过复习要使学生理解加速度的含义,弄清加速度与速度、加速度与速度改变量的区别.对于运动图象的复习,要使学生理解图象的含义,能根据运动图象获取有关的运动信息.
12.羚羊从静止开始奔跑,经过50 m距离能加速到最大速度25 m/s,并能维持一段较长的时间;猎豹从静止开始奔跑,经过60 m的距离能加速到最大速度30 m/s,以后只能维持这个速度4.0 s.设猎豹距离羚羊x m时开始攻击,羚羊则在猎豹开始攻击后1.0 s才开始奔跑,假定羚羊和猎豹在加速阶段分别做匀加速运动,且均沿同一直线奔跑.求:
(1)猎豹要在其最大速度减速前追到羚羊,x值应在什么范围?
(2)猎豹要在其加速阶段追上羚羊,x值应在什么范围?
[解析] (1)设猎豹在最大速度将要减速时恰追上羚羊,则猎豹运动的位移和时间分别为
s1=s10+v1mt1″=60 m+30×4.0 m=180 m
t1=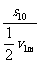 +t1″=
+t1″=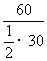 s+4.0 s=8.0 s
s+4.0 s=8.0 s
则羚羊运动的时间为
t2=t1-1=7.0 s
羚羊加速的时间为
t2′=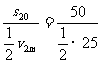 s=4.0 s
s=4.0 s
故羚羊匀速运动的时间为
t2″=t2-t2′=3.0 s
羚羊的位移为
s2=s20+v2mt2″=50 m+25×3.0 m=125 m
则为使猎豹能在从最大速度减速前追上羚羊,应有x≤s1-s2=55 m
(2)猎豹加速的时间和位移分别为
t1′=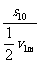 =4.0 s
=4.0 s
s1′=60 m
羚羊加速运动的加速度和位移分别为
a2=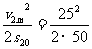 m/s2 =6.25 m/s2s2′=
m/s2 =6.25 m/s2s2′=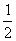 a2(t1′-1)2=
a2(t1′-1)2=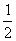 ×6.25×3.02
m=28.1 m
×6.25×3.02
m=28.1 m
为使猎豹能在加速阶段追上羚羊,应有x≤s1′-s2′=31.9 m
[答案] (1)x≤55 m;(2)x≤31.9 m
●教学建议
11.某人在高100 m的塔顶,每隔0.5 s由静止释放一个金属小球.取g=10 m/s2,求:
(1)空中最多能有多少个小球?
(2)在空中最高的小球与最低的小球之间的最大距离是多少?(不计空气阻力)
[解析] 由H=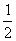 gt2,那么第一个球从静止释放到着地的时间t=
gt2,那么第一个球从静止释放到着地的时间t=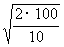 s=4.47 s.则释放小球个数就是空中小球数.则n=
s=4.47 s.则释放小球个数就是空中小球数.则n=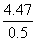 ,对n取整数加1,所以N=8+1=9(个).当最低球着地前一瞬间,最低球与最高球之间有最大距离,则由h=
,对n取整数加1,所以N=8+1=9(个).当最低球着地前一瞬间,最低球与最高球之间有最大距离,则由h=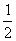 gt2=
gt2=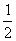 ×10×0.472
m=1.10 m,所以Δs=H-h=100 m-1.10
m=98.90m.
×10×0.472
m=1.10 m,所以Δs=H-h=100 m-1.10
m=98.90m.
[答案] (1)9个;(2)98.90m
10.一辆汽车以54 km/h的速度正常行驶,来到路口遇上红灯,汽车先以0.5 m/s2的加速度做匀减速直线运动,在路口停了2 min,接着又以0.3 m/s2的加速度做匀加速直线运动并恢复到原来的速度正常行驶.求这辆汽车通过这个路口所延误的时间.
[解析] 汽车减速运动的位移和时间分别为
s1=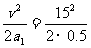 m=225 m
m=225 m
t1=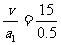 s=30 s
s=30 s
汽车加速到正常速度通过的位移及所用时间分别为
s2=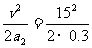 m=375 m
m=375 m
t2=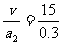 s=50 s
s=50 s
汽车正常通过这段位移用的时间为
t=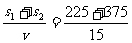 s=40 s
s=40 s
则汽车因停车延误的时间为
Δt=120 s+30 s+50 s-40 s=160 s
[答案] 160 s
9.两辆完全相同的汽车,沿水平路面一前一后均以20 m/s的速度前进,若前车突然以恒定的加速度刹车,在它刚停车时,后车以前车刹车时的加速度的2倍开始刹车,已知前车在刹车过程所行驶的距离为100 m,若要保证两车在上述情况下不相撞,则两车在匀速行驶时保持的最小距离是 .
[解析] 设前车刹车过程的位移为s1,加速度为a,则有:
s1=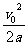 =100 m
=100 m
在前车刹车的过程中,后车仍以v0匀速运动,在这段时间内它的位移为
s2′=2s1=200 m
后车刹车的位移为
s2″=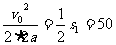 m
m
故从前车开始刹车到后车也停下来,后车的总位移为
s2=s2′+s2″=250 m
两车匀速运动时它们间的距离为
Δs=s2-s1=250 m-100 m=150 m
[答案] 150 m
8.某百货大楼一、二楼之间有一部正在向上运动的自动扶梯,某人以相对扶梯的速度v沿楼梯向上跑,数得扶梯有n1级;到二楼后他又返回以相同的相对扶梯的速度v沿梯子向下跑,数得扶梯有n2级,那么该扶梯在一、二楼间实际有______级.
[解析] 设两台阶间沿楼梯斜面的距离为l,一、二楼间共有n级台阶,设电梯的速度为v′,则有
n1=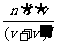
n2=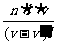
求得n=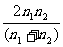
[答案] 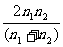
7.汽车在平直的公路上做匀加速直线运动,经过第一棵树时速度为1 m/s,经过第三棵树时速度为7 m/s,若每两棵树间距相等,那么经过第二棵树时的速度为______m/s;若每两棵树间距为10 m,则从第一棵树到第三棵树运动的时间是______s,汽车的加速度为________m/s2.
[解析] 利用匀变速直线运动中点速度vs/2=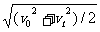 这一推论,将v0=1 m/s,vt=7 m/s代入,得vs/2=5 m/s.从第一棵树至第三棵树的平均速度
这一推论,将v0=1 m/s,vt=7 m/s代入,得vs/2=5 m/s.从第一棵树至第三棵树的平均速度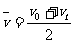 =4 m/s,故时间t=
=4 m/s,故时间t=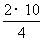 s=5 s.汽车的加速度a=
s=5 s.汽车的加速度a=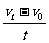 =1.2 m/s2.
=1.2 m/s2.
[答案] 5;5;1.2
6.由静止开始做匀加速直线运动的物体,当经过s位移的速度是v时,那么经过位移为2s时的速度是______.
[解析] 由vt2-v02=2as得
v2=2as
v′2=2a·2s=2v2
所以v′=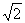 v
v
[答案] 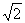 v
v
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com