
5.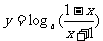
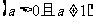 的定义域为 ( )
的定义域为 ( )
A.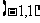 B.
B.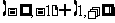 C.
C.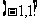 D.R
D.R
4.已知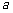 、
、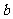 、
、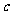 满足
满足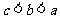 且
且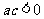 ,那么下列式子一定成立的是
( )
,那么下列式子一定成立的是
( )
A. B.
B.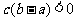 C.
C.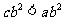 D.
D.
3.不等式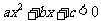 (这里
(这里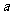
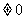 )恒成立的条件是
( )
)恒成立的条件是
( )
A. B.
B. C.
C.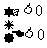 D.
D.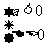
2.不等式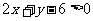 表示的平面区域在直线
表示的平面区域在直线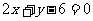 ( )
( )
A.左上方 B.右上方 C.左下方 D.右下方
1. 不等式(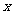 +3)(
+3)(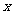 -1)<0的解为
( )
-1)<0的解为
( )
A.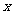
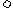
 B. 1
B. 1
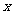
 3
C.
-3
3
C.
-3
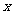
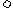 1 D.
1 D. 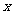
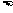 1且
1且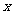 ¹-3
¹-3
22. 解:(Ⅰ)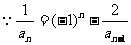 ,
,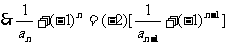 ,……2分
,……2分
又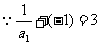 ,
,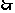 数列
数列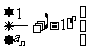 是首项为
是首项为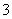 ,公比为
,公比为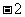 的等比数列.…3分
的等比数列.…3分
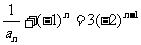 , 即
, 即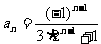 . ……………4分
. ……………4分
(Ⅱ)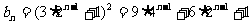 .
.
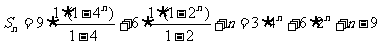 . ………………8分
. ………………8分
(Ⅲ)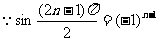 ,
,
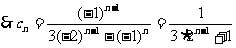 .
……………………10分
.
……………………10分
当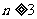 时,则
时,则
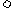

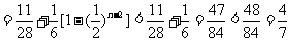 .
.
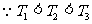 ,
, 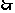 对任意的
对任意的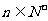 ,
,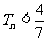 . ………………………12分
. ………………………12分
21. 解:(1)由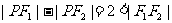 知,点P的轨迹E是以F1、F2为焦点的双曲线的右支,由
知,点P的轨迹E是以F1、F2为焦点的双曲线的右支,由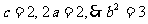 ,故轨迹E的方程为
,故轨迹E的方程为
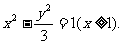 ………………………………………………………………2分
………………………………………………………………2分
(错误!未找到引用源。)当直线l的斜率存在时,设直线方程为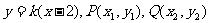 ,与双曲线方程联立消y得
,与双曲线方程联立消y得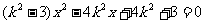 ,
,
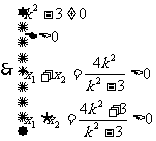
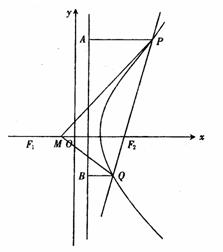 解得k2 >3
………………………………………………………………………………4分
解得k2 >3
………………………………………………………………………………4分


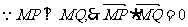 ,
,
故得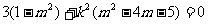 对任意的
对任意的
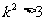 恒成立,
恒成立,
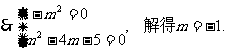
∴当m =-1时,MP⊥MQ. ………………………………………………6分
(错误!未找到引用源。)当直线l的斜率不存在时,由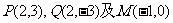 知结论也成立,
知结论也成立,
综上,当m =-1时,MP⊥MQ. ………………………………………………7分
(2)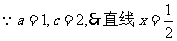 是双曲线的右准线,
是双曲线的右准线,
 由双曲线定义得:
由双曲线定义得: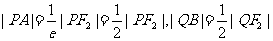 ,………………8分
,………………8分
方法一: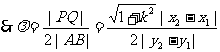
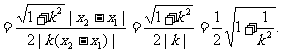
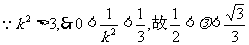 ,……………10分
,……………10分
注意到直线的斜率不存在时,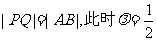 ,……11分
,……11分
综上,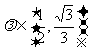 ………………………………………………12分
………………………………………………12分
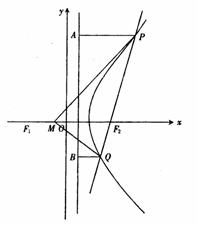
方法二:设直线PQ的倾斜角为θ,由于直线PQ与双曲线右支有二个交点,
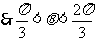 ,过Q作QC⊥PA,垂足为C,则
,过Q作QC⊥PA,垂足为C,则
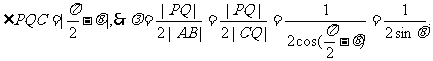 ……11分
……11分
由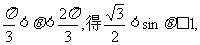
故: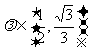 ………………12分
………………12分
20.
(1)∵当a=1时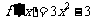 ,令
,令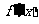 =0,得x=-1或x=1…………2分
=0,得x=-1或x=1…………2分
当x∈(-1,1)时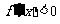 ,当
,当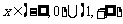 时
时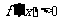
∴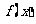 在
在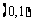 上单调递减,在
上单调递减,在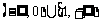 上单调递增,
上单调递增,
∴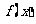 的极小值为
的极小值为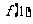 =-2. …………………………………………………4分
=-2. …………………………………………………4分
(2)∵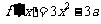
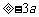 ………………………………………………………6分
………………………………………………………6分
∴要使直线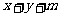 =0对任意的
=0对任意的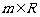 总不是曲线
总不是曲线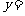
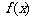 的切线,
的切线,
当且仅当-1<-3a,
∴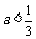 .…………………………………………………………………………8分
.…………………………………………………………………………8分
(3)因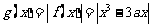 在[-1,1]上为偶函数,故只求在[0,1]上最大值…9分
在[-1,1]上为偶函数,故只求在[0,1]上最大值…9分
当 时
时 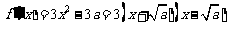
错误!未找到引用源。 .当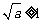 ,即
,即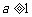 时
时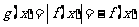 ,
,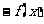 在
在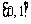 上单调递增,
上单调递增,
此时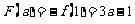 ……………………………………………………………10分
……………………………………………………………10分
错误!未找到引用源。. 当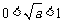 ,且
,且
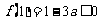 即
即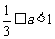 时,
时,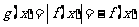 在
在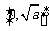 上单调递增,在
上单调递增,在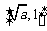 上单调递减,
上单调递减,
故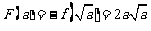 .…………………………………………………………11分
.…………………………………………………………11分
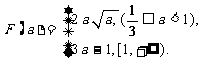 ………………………………………………12分
………………………………………………12分
19. 解法1:(1)延长B1E交BC于F,
∵ΔB1EC1∽ΔFEB, BE=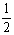 EC1
EC1
∴BF=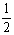 B1C1=
B1C1=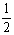 BC,从而F为BC的中点. ………………2分
BC,从而F为BC的中点. ………………2分
∵G为ΔABC的重心,∴A、G、F三点共线,且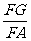 =
=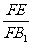 =
=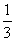 ,
,
∴GE∥AB1,
又GE 侧面AA1B1B,
侧面AA1B1B,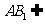 侧面AA1B1B, ∴GE∥侧面AA1B1B …………4分
侧面AA1B1B, ∴GE∥侧面AA1B1B …………4分
(2)在侧面AA1B1B内,过B1作B1H⊥AB,垂足为H,∵侧面AA1B1B⊥底面ABC,∴B1H⊥底面ABC.又侧棱AA1与底面ABC成600的角, AA1= 2,
∴∠B1BH=600,BH=1,B1H=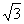 ………………………………6分
………………………………6分
在底面ABC内,过H作HT⊥AF,垂足为T,连B1T.由三垂线定理有
B1T⊥AF,又平面B1GE与底面ABC的交线为AF,
∴∠B1TH为所求二面角的平面角………………………………………………8分
∴AH=AB+BH=3,∠HAT=300, ∴HT=AHsin300=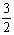 ,
,
在RtΔB1HT中,tan∠B1TH=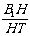 =
=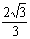 ………………10分
………………10分
从而平面B1GE与底面ABC所成锐二面角的大小为arctan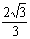 ………………12分
………………12分
解法2:(1)∵侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成600的角,
∴∠A1AB=600,又AA1= AB= 2,取AB的中点O,则AO⊥底面ABC.
以O为原点建立空间直角坐标系O-xyz如图,…………………………1分
则A(0,-1,0),B(0,1,0),C(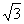 ,0,0),
,0,0),
A1(0,0,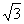 )B1(0,2,
)B1(0,2,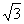 ),C1(
),C1(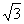 ,1,
,1,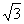 ).
).
∵G为ΔABC的重心,∴G(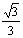 ,0,0), ∵
,0,0), ∵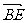 =
=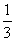
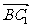
∴E(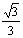 ,1,
,1,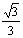 )∴
)∴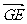 =(0,1,
=(0,1,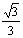 )=
)=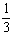
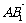 ,
,
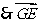 ∥
∥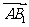 即GE∥AB1…………………………………………………………3分
即GE∥AB1…………………………………………………………3分
又GE 侧面AA1B1B,
侧面AA1B1B,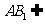 侧面AA1B1B, ∴GE∥侧面AA1B1B ………… 4分
侧面AA1B1B, ∴GE∥侧面AA1B1B ………… 4分
(2)设平面B1GE的法向量为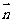 =(a,b,c),
=(a,b,c),
则由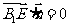 及
及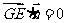 得
得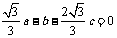 ;
;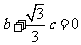 .
.
可取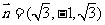 ………………………………………..…7分
………………………………………..…7分
又底面ABC的法向量为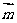 =(0,0,1),………………………………9分
=(0,0,1),………………………………9分
设平面B1GE与底面ABC所成锐二面角的大小为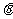 ,
,
则cos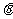 =
=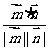 =
=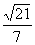 , ……………………………………………11分
, ……………………………………………11分
∴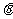 =arccos
=arccos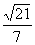 .………………………………………………………………12分
.………………………………………………………………12分
18. 解:(1)记“从袋中摸出的2个球中含有红球”为事件A
则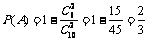 ………………………………………………………………4分
………………………………………………………………4分
(2)记“从袋中摸出的2个球都是红球”为事件B
则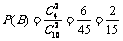 ………………………………………………………………6分
………………………………………………………………6分
3次摸球恰好有两次中大奖相当于作了3次独立重复实验
则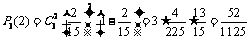 ………………………………8分
………………………………8分
(3)中大奖的次数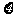 可能取的值为0,1,2,3
可能取的值为0,1,2,3
∴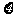 的数学期望为
的数学期望为
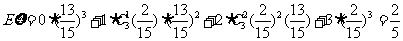 ………………12分
………………12分
或E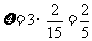
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com