
7.已知 是椭圆
是椭圆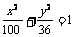 上的一点,若
上的一点,若 到椭圆右准线的距离是
到椭圆右准线的距离是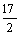 ,则点
,则点 到左焦点的距离( )
到左焦点的距离( )
A.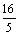 B.
B.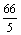 C.
C.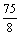 D.
D.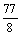
6.若椭圆两准线间的距离等于焦距的4倍,则这个椭圆的离心率为 ( )
A.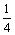 B.
B.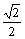 C.
C.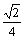 D.
D. 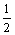
5.椭圆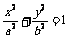 和
和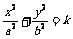
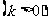 具有 ( )
具有 ( )
A.相同的离心率 B.相同的焦点 C.相同的顶点 D.相同的长、短轴
4.设定点F1(0,-3)、F2(0,3),动点P满足条件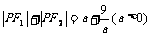 ,则点P的轨迹是( )
,则点P的轨迹是( )
A.椭圆 B.线段 C.不存在 D.椭圆或线段
3.若方程x2+ky2=2表示焦点在y轴上的椭圆,则实数k的取值范围为 ( )
A.(0,+∞) B.(0,2) C.(1,+∞) D.(0,1)
2.若椭圆的两焦点为(-2,0)和(2,0),且椭圆过点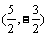 ,则椭圆方程是 ( )
,则椭圆方程是 ( )
A.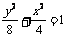 B.
B.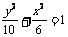 C.
C.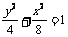 D.
D.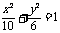
1.下列命题是真命题的是 ( )
A.到两定点距离之和为常数的点的轨迹是椭圆
B.到定直线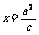 和定点F(c,0)的距离之比为
和定点F(c,0)的距离之比为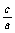 的点的轨迹是椭圆
的点的轨迹是椭圆
C.到定点F(-c,0)和定直线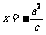 的距离之比为
的距离之比为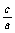 (a>c>0)的点的轨迹
是左半个椭圆
(a>c>0)的点的轨迹
是左半个椭圆
D.到定直线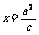 和定点F(c,0)的距离之比为
和定点F(c,0)的距离之比为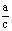 (a>c>0)的点的轨迹是椭圆
(a>c>0)的点的轨迹是椭圆
25.(14分)
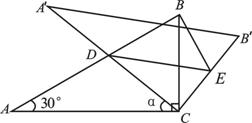
如图,将含30°角的直角三角板ABC(∠A=30°)绕其直角顶点C逆时针旋转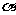 角(
角(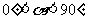 ),得到Rt△
),得到Rt△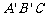 ,
,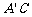 与AB交于点D,过点D作DE∥
与AB交于点D,过点D作DE∥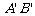 交
交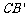 于
于
点E,连结BE.易知,在旋转过程中,△BDE为直角三角形. 设 BC=1,AD=x,△BDE的
面积为S.
(1)当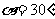 时,求x的值.
时,求x的值.
(2)求S与x 的函数关系式,并写出x的取值范围;
 (3)以点E为圆心,BE为半径作⊙E,当S=
(3)以点E为圆心,BE为半径作⊙E,当S=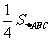 时,判断⊙E与
时,判断⊙E与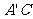 的位置关
的位置关
系,并求相应的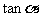 值.
值.
24.(13分)
在平面直角坐标系中,点A、B的坐标分别为(10,0),(2,4).
(1)若点C是点B关于x轴的对称点,求经过O、C、A三点的抛物线的解析式;
(2)若P为抛物线上异于C的点,且△OAP是直角三角形,请直接写出点P的坐标;
(3)若抛物线顶点为D,对称轴交x轴于点M,探究:抛物线对称轴上是否存在异于D的
点Q,使△AQD是等腰三角形,若存在,请求出点Q的坐标;若不存在,请说明理由.
23.(12分)
某市市政公司为绿化一片绿化带,计划购买甲、乙两种树苗共1000株,单价分别为60元、
80元,其成活率分别为90%、95%
(1)若购买树苗共用68000元,求甲、乙两种树苗各多少株?
(2)若希望这批树苗的成活率不低于93%,且购买树苗的费用最低,应如何选购树苗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com