
9、两个正数a
、b的等差中项是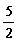 ,一个等比中项是
,一个等比中项是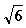 ,且
,且 则椭圆
则椭圆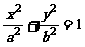 的离心率e等于( )
的离心率e等于( )
A.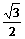 B.
B.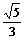 C.
C. 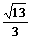 D.
D.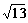
8、已知球O的半径为2cm,A、B、C为球面上三点, A与B、B与C的球面距离都是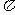 cm,A与C的球面距离为
cm,A与C的球面距离为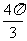 cm,那么三棱锥O-ABC的体积为( )
cm,那么三棱锥O-ABC的体积为( )
A.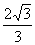 cm3 B.
cm3 B.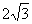 cm3 C.
cm3 C.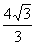 cm3 D.
cm3 D.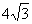 cm3
cm3
7、抛物线 上的点到直线
上的点到直线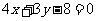 距离的最小值是( )
距离的最小值是( )
A. B.
B.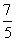 C.
C.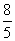 D.
D.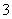
6、已知向量 满足
满足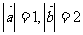 ,
,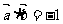 ,则向量
,则向量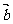 在向量
在向量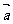 方向上的投影是 ( )
方向上的投影是 ( )
A.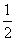 B.
B. C.
C.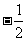 D.
D.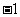
5、函数f(x)=|sinx|的一个单调递增区间是( )
A.[-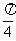 ,
,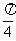 ] B.[
] B.[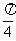 ,
,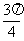 ] C.[
] C.[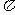 ,
,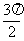 ] D.[
] D.[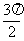 ,2
,2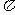 ]
]
4、过空间一定点P的直线中,与长方体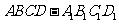 的12条棱所在直线成等角的直线共有( )
的12条棱所在直线成等角的直线共有( )
A.0条 B.1条 C.4条 D.无数条
3、某汽车经销商在国庆长假中销售了高级轿车54辆,中级轿车108辆,经济型轿车162辆,现要对其中36辆车进行售后调查,为了使调查更具代表性,则应选( )
A. 高级轿车4辆,中级轿车14辆,经济型轿车18辆
B. 高级轿车6辆,中级轿车12辆,经济型轿车18辆
C. 高级轿车8辆,中级轿车12辆,经济型轿车16辆
D. 高级轿车10辆,中级轿车12辆,经济型轿车14辆
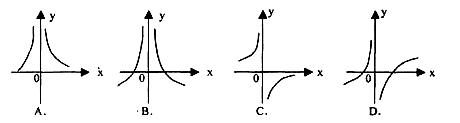
2、函数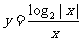 的大致图象是 ( )
的大致图象是 ( )
1、已知集合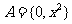 ,
, ,若
,若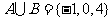 ,则
,则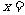 ( )
( )
A.4 B.2 C.  D.0或2
D.0或2
22. (本小题满分12分)(理科)已知函数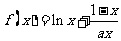 ,其中
,其中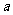 为大于零的常数.
为大于零的常数.
(Ⅰ)若函数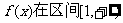 内调递增,求a的取值范围;
内调递增,求a的取值范围;
(Ⅱ)求函数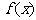 在区间[1,2]上的最小值;
在区间[1,2]上的最小值;
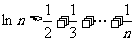
(Ⅲ)求证:对于任意的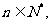 n>1时,都有
n>1时,都有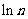 >
>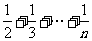 成立.
成立.
答案: 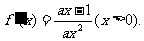 ……………………………….2分
……………………………….2分
(Ⅰ)当a=1时,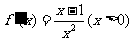 .
.
当x>1时,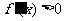 ;当0<x<1时,
;当0<x<1时,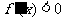 .
.
∴f(x)的增区间为(1,+∞),减区间为(0,1). …………………4分
(Ⅱ)当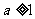 时,
时,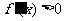 在(1,2)上恒成立,这时
在(1,2)上恒成立,这时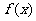 在[1,2]上为增函数
在[1,2]上为增函数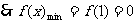 .
.
当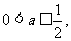
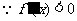 在(1,2)上恒成立,
在(1,2)上恒成立,
这时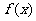 在[1,2]上为减函数
在[1,2]上为减函数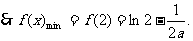
当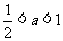 时, 令
时, 令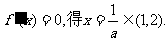
又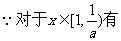
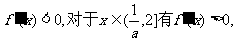
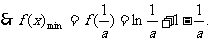 ……………………………………6分
……………………………………6分
综上,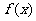 在[1,2]上的最小值为
在[1,2]上的最小值为
①当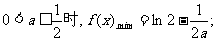
②当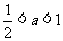 时,
时,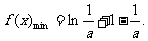
③当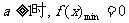 …………………………………………
8分
…………………………………………
8分
(Ⅲ)由(Ⅰ)知函数 上为增函数,
上为增函数,
当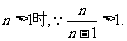
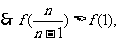
即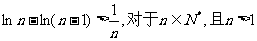 恒成立 ……………………10分
恒成立 ……………………10分
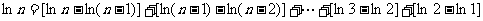
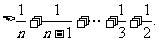
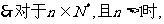
 恒成立.
恒成立.
………………………………………12分
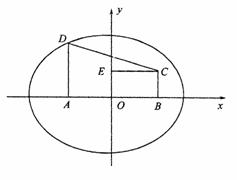
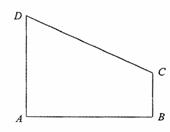 (文科)如图,直角梯形ABCD中∠DAB=90°,AD∥BC,AB=2,AD=
(文科)如图,直角梯形ABCD中∠DAB=90°,AD∥BC,AB=2,AD=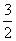 ,BC=
,BC=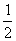 .椭圆G以A、B为焦点且经过点D.
.椭圆G以A、B为焦点且经过点D.
(Ⅰ) 建立适当坐标系,求椭圆G的方程;
(Ⅱ)若点E满足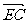
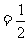
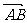 ,问是否存在不平行AB的直线l与椭圆G交于M、N两点且
,问是否存在不平行AB的直线l与椭圆G交于M、N两点且 ,若存在,求出直线l与AB夹角正切值的范围,若不存在,说明理由.
,若存在,求出直线l与AB夹角正切值的范围,若不存在,说明理由.
答案:(Ⅰ)如图,以AB所在直线为x轴,AB中垂线为y轴建立直角坐标系, A(-1,0),B(1,0).
A(-1,0),B(1,0).
 设椭圆方程为
设椭圆方程为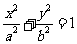 .
.
令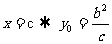 ,
,
∴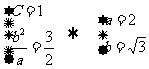 .
.
∴ 椭圆C的方程是: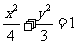 ………………………6分
………………………6分
(Ⅱ)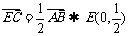 ,l⊥AB时不符;
,l⊥AB时不符;
设l:y=kx+m(k≠0),
由 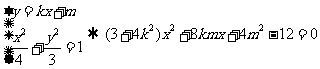 ……………….8分
……………….8分
M、N存在

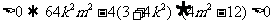
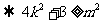 .
.
设M(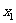 ,
,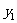 ),N(
),N(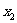 ,
,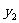 ),MN的中点F(
),MN的中点F(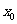 ,
,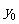 )
)
∴ 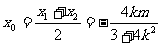 ,
,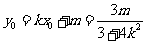 ………..10分
………..10分
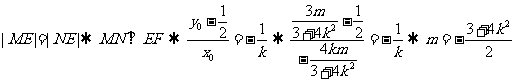 ,
,
∴ 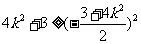 ,∴
,∴  ,
,
∴ 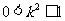 , ∴
, ∴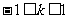 且
且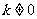 .
.
∴ l与AB的夹角的范围是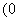 ,
,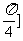 .………………………….12分
.………………………….12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com