
25.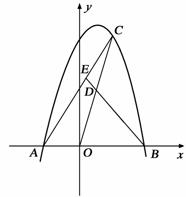 已知:如图,抛物线
已知:如图,抛物线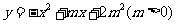 与
与
轴交于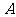 、
、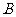 两点,点
两点,点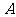 在点
在点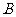 的左边,
的左边,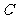 是抛物线
是抛物线
上一动点(点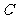 与点
与点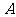 、
、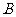 不重合),
不重合),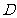 是
是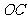 中点,
中点,
连结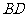 并延长,交
并延长,交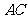 于点
于点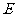 .
.
(1)求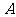 、
、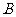 两点的坐标(用含
两点的坐标(用含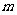 的代数式表示);
的代数式表示);
(2)求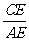 的值;
的值;
(3)当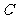 、
、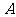 两点到
两点到 轴的距离相等,且
轴的距离相等,且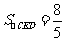 时, 求抛物线和直线
时, 求抛物线和直线 的解析式.
的解析式.
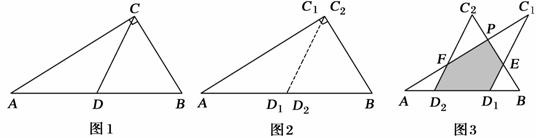
24.如图1,一张三角形纸片ABC,∠ACB=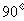 ,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成
,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成 两个三角形(如图2).将
两个三角形(如图2).将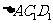 沿直线
沿直线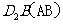 方向平移(点
方向平移(点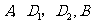 始终在同一直线上),当点
始终在同一直线上),当点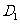 与点B重合时停止平移.在平移的过程中,
与点B重合时停止平移.在平移的过程中, 交于点E,
交于点E,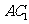 与
与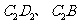 分别交于点F、P.
分别交于点F、P.
(1)当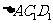 平移到如图3所示位置时,猜想
平移到如图3所示位置时,猜想 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想;
(2)设平移距离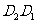 为x,
为x, 重叠(阴影)部分面积为y,试求y与x的函数关系式,并写出自变量x的取值范围.
重叠(阴影)部分面积为y,试求y与x的函数关系式,并写出自变量x的取值范围.
23.已知抛物线y=x²-4x+1.将此抛物线沿x轴方向向左平移4个单位长度,得到一条新的抛物线.
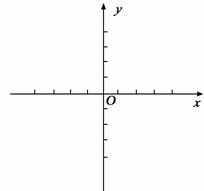 (1)求平移后的抛物线解析式;
(1)求平移后的抛物线解析式;
(2)由抛物线对称轴知识我们已经知道:直线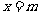 ,即为过点(m,0)平行于
,即为过点(m,0)平行于 轴的直线,类似地,直线
轴的直线,类似地,直线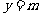 ,即为过点(0,m)平行于
,即为过点(0,m)平行于 轴的直线.请结合图象回答:当直线y=m与这两条抛物线有且只有四个交点,实数m的取值范围;
轴的直线.请结合图象回答:当直线y=m与这两条抛物线有且只有四个交点,实数m的取值范围;
(3)若将已知的抛物线解析式改为y=x²+bx+c(b<0),并将此抛物线沿x轴向左平移
-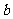 个单位长度,试回答(2)中的问题.
个单位长度,试回答(2)中的问题.
21.国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的条形统计图(部分)如图所示,其中分组情况是:
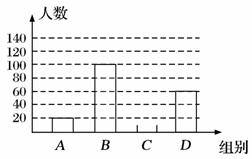 A组:
A组: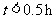 ;
;
B组: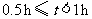
C组: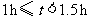
D组:
请根据上述信息解答下列问题:
(1)C组的人数是 ;
(2)将条形统计图补充完整;
(3)本次调查数据的中位数落在 组内;
(4)若该区约有24 000名初中学生,请估计其中达国家规定体育活动时间的人约有多少?
20.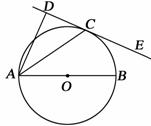 已知:如图, AB是⊙O的直径,直线CD与⊙O相切于
已知:如图, AB是⊙O的直径,直线CD与⊙O相切于
点C,AC平分∠DAB.
(1) 求证:AD⊥DC;
(2) 若AD=2,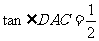 ,求
,求 直径AB的长.
直径AB的长.
19.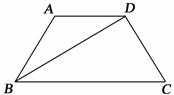 如图,在梯形ABCD中,AD∥BC,
如图,在梯形ABCD中,AD∥BC, 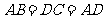 ,
,
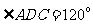 ,若
,若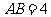 .
.
求梯形ABCD的面积.
18.列方程或方程组解应用题:
某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?
17.已知:图中的曲线是反比例函数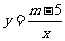 (
(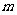 为常数)图象 的一支.
为常数)图象 的一支.
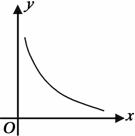
(1)这个反比例函数图象的另一支在第几象限?常数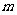 的取值
的取值
范围是什么?
(2)若该函数的图象与正比例函数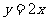 的图象在第一象内限
的图象在第一象内限
的交点为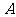 ,过
,过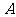 点作
点作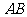
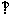
 轴于
轴于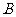 ,当
,当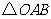 的面积
的面积
为4时,求点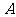 的坐标及反比例函数的解析式.
的坐标及反比例函数的解析式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com