
7.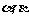 是两个相交平面,a
是两个相交平面,a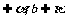 ,a与b之间的距离为d1,
,a与b之间的距离为d1,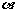 与
与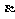 之间的距离为d2,则( ) A.d1=d2 B.d1>d2 C.d1<d2 D.d1
之间的距离为d2,则( ) A.d1=d2 B.d1>d2 C.d1<d2 D.d1 d2
d2
6. 设平面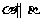 ,A
,A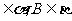 ,C是AB的中点,当A、B分别在
,C是AB的中点,当A、B分别在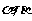 内运动时,那么所有的动点C ( )
内运动时,那么所有的动点C ( )
A. 不共面 B.当且仅当A、B分别在两条直线上移动时才共面
C. 当且仅当A、B分别在两条给定的异面直线上移动时才共面 D. 不论A、B如何移动,都共面
5.下列四个命题:①分别在两个平面内的两直线平行;②若两个平面平行,则其中一个平面内的任何一条直线必平行于另一平面;③如果一个平面内的两条直线平行于另一个平面,则这两个平面平行; ④如果一个平面内的任何一条直线都平行另一个平面,则这两个平面平行. 其中正确命题是( )
A. ①、② B. ②、④ C. ①、③ D. ②、③
4.已知a,b是异面直线,且a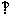 平面
平面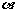 ,b
,b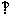 平面
平面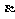 ,则
,则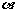 与
与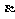 的关系是( )
的关系是( )
A. 相交 B. 重合 C. 平行 D. 不能确定
3. 命题:①与三角形两边平行的平面平行于是三角形的第三边; ②与三角形两边垂直的直线垂直于第三边;③与三角形三顶点等距离的平面平行这三角形所在平面. 其中假命题的个数为( )
A.0 B.1 C.2 D.3
2. 设直线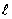 ,m,平面
,m,平面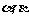 ,下列条件能得出
,下列条件能得出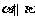 的是( )
的是( )
A.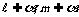 ,且
,且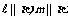 B.
B. 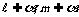 ,且
,且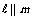
C. 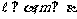 ,且
,且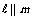 D.
D. 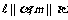 ,且
,且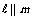
1.下列命题中正确的命题是( )
①平行于同一直线的两平面平行; ②平行于同一平面的两平面平行;
③垂直于同一直线的两平面平行; ④与同一直线成等角的两平面平行.
A.①和② B.②和③ C.③和④ D.②和③和④
21. 如图O是正方体下底面ABCD中心,B1H^D1O,H为垂足.
如图O是正方体下底面ABCD中心,B1H^D1O,H为垂足.
求证:B1H  平面AD1C.
平面AD1C.
 必修2
第1章
立体几何初步
必修2
第1章
立体几何初步
§1.2.4 平面与平面的位置关系
重难点:了解直线与平面的位置关系,在判定和证明直线与平面的位置关系时,除了能熟练运用判定定理和性质定理外,还要充分利用定义;线面关系的判定和证明,要注意线线关系、线面关系的转化.
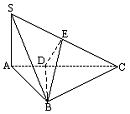
经典例题:如图,在四面体S-ABC中, SA⊥底面ABC,AB⊥BC.DE垂直平分SC, 且分别交AC、SC于D、E. 又SA=AB,SB=BC.求以BD为棱, 以BDE与BDC为面的二面角的度数.
当堂练习:
20.M,N,P分别为空间四边形ABCD的边AB,BC,CD上的点,且AM:MB=CN:NB=CP:PD.
 求证:(1)AC||平面MNP,BD||平面MNP; (2)平面MNP与平面ACD的交线||AC.
求证:(1)AC||平面MNP,BD||平面MNP; (2)平面MNP与平面ACD的交线||AC.
19. 如图,空间四边形ABCD被一平面所截,截面EFGH是一个矩形,
如图,空间四边形ABCD被一平面所截,截面EFGH是一个矩形,
(1)求证:CD||平面EFGH;
(2)求异面直线AB,CD所成的角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com