20.(本小题满分14分)

已知函数对任意实数均有，其中常数为负数，且在区间上有表达式.w_w w. k#s5_

(1)求，的值；

(2)写出在上的表达式，并讨论函数在上的单调性；

(3)求出在上的最小值与最大值，并求出相应的自变量的取值. w_w*w.k_s_

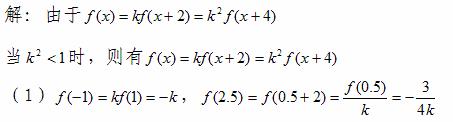
(2)当时，

当时，

当时，

c. 当时，

此时：

19.(本题满分12分)

某营养师要求为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物，6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物，6个单位的蛋白质和10个单位的维生素C.另外，该儿童这两餐需要的营状中至少含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.

如果一个单位的午餐、晚餐的费用分别是2.5元和4元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预订多少个单位的午餐和晚餐？

解：设为该儿童分别预订个单位的午餐和个单位的晚餐，设费用为F，则F，由题意知：

画出可行域：

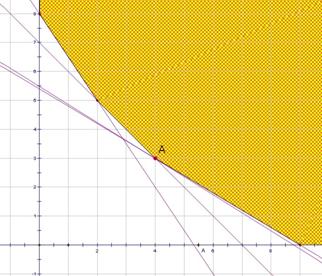变换目标函数：

18.(本小题满分14分)

如图4，弧AEC是半径为的半圆，AC为直径，点E为弧AC的中点，点B和点C为线段AD的三等分点，平面AEC外一点F满足FC平面BED,FB=

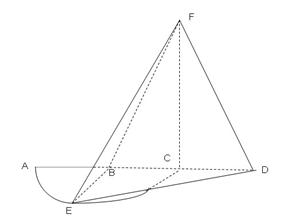(1)证明：EBFD

(2)求点B到平面FED的距离.

(1)证明：点E为弧AC的中点

17.(本小题满分12分)

某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中，随机抽取了100名电视观众，相关的数据如下表所示：

16．(本小题满分14分)

设函数，，，且以为最小正周期．

(1)求；w_w(2)求的解析式；(3)已知，求的值．w_w*w.k_s_

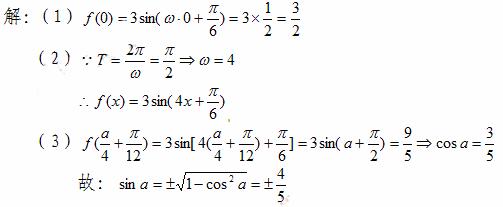
15.(坐标系与参数方程选做题)在极坐标系中，曲线与的交点的极坐标为　　　 .

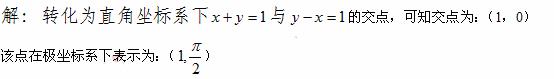
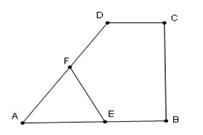
14.(几何证明选讲选做题)如图3，在直角

梯形ABCD中，DC∥AB,CB,AB=AD=,CD=,

点E,F分别为线段AB,AD的中点，则EF= 　

解：连结DE，可知为直角三角形。则EF是斜边上的中线，等于斜边的一半，为.

13．已知a，b，c分别是△ABC的三个内角A，B，C所对的边，若a=1，b=，A+C=2B，则sinA=　　　　　 . w_w w. k#s5_

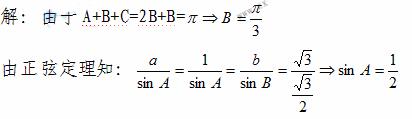
(二)选做题(14、15题，考生只能从中选做一题)

12．某市居民2005-2009年家庭年平均收入x(单位：万元)与年平均支出Y(单位：万元)的统计资料如下表所示：w_w w. k#s5_

根据统计资料，居民家庭年平均收入的中位数是　 13　　 ，家庭年平均收入与年平均支出有

　　 Y=x-3　　 线性相关关系.

(一)必做题(11~13题)

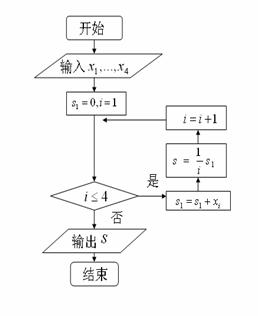
11.某城市缺水问题比较突出，为了制定节水管

理办法，对全市居民某年的月均用水量进行了

抽样调查，其中4位居民的月均用水量分别为

(单位：吨)。根据图2所示的程序框图，若分

别为1，1.5，1.5，2，则输出的结果为　 　.

解析：