
8.直线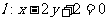 过双曲线的左焦点F1和一个虚顶点B,该双曲线的离心率为(
)
过双曲线的左焦点F1和一个虚顶点B,该双曲线的离心率为(
)
A.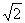 B.
B.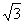 C.
C. D.2
D.2
7. 先后抛掷两枚均匀的骰子,骰子朝上的点数分别为X,Y,则满足 的概率是( )
的概率是( )
A.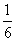 B.
B.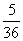 C.
C.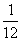 D.
D.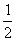
6.设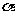 、
、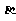 为两个不同的平面,l、m为两条不同的直线,且l
为两个不同的平面,l、m为两条不同的直线,且l
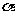 ,m
,m
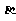 ,有如下的两个命题:①若
,有如下的两个命题:①若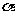 ∥
∥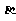 ,则l∥m;②若l⊥m,则
,则l∥m;②若l⊥m,则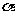 ⊥
⊥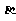 .那么( )
.那么( )
A.①是真命题,②是假命题 B.①是假命题,②是真命题
C.①②都是真命题 D.①②都是假命题
5.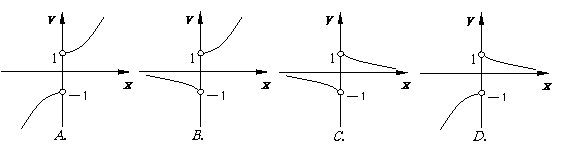 函数
函数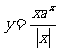
 的图象的大致形状是 ( )
的图象的大致形状是 ( )
4.若x∈(0,2π],则使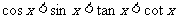 成立的x取值范围是( )
成立的x取值范围是( )
A.(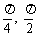 )
B.(
)
B.(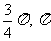 ) C.(
) C.(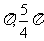 )
D.(
)
D.(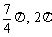 )
)
2. 若复数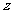 满足
满足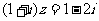 ,则复数
,则复数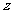 在复平面上的对应点在( )
在复平面上的对应点在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
3.若样本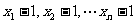 的平均数是5,方差为2,则对于样本
的平均数是5,方差为2,则对于样本
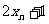 ,下列结论中正确的是( )
,下列结论中正确的是( )
A.平均数是5,方差是2 B.平均数是10,方差是2
C.平均数是10,方差是8 D.平均数是13,方差是8
1.设集合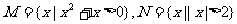 则( )
则( )
A.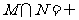 B.
B.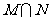
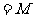
C.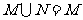 D.
D.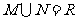
22、(本小题满分12分)
已知定点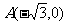 ,B是圆
,B是圆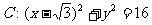 (C为圆心)上的动点,AB的垂直平分线与BC交于点E。
(C为圆心)上的动点,AB的垂直平分线与BC交于点E。
(Ⅰ)求动点E的轨迹方程;
(Ⅱ)设直线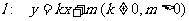 与E的轨迹交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:
与E的轨迹交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求: OPQ面积的最大值及此时直线
OPQ面积的最大值及此时直线 的方程。
的方程。
w@w.w.k~s.5*p;m
21、(本小题满分12分)
已知函数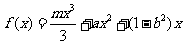 ,
,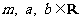 .
.
(Ⅰ)求函数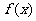 的导函数
的导函数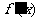 ;
;
(Ⅱ)当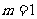 时,若函数
时,若函数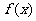 是
是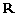 上的增函数,求
上的增函数,求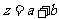 的最小值;
的最小值;
(Ⅲ)当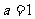 ,
,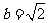 时,函数
时,函数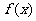 在
在 上存在单调递增区间,求
上存在单调递增区间,求 的取值范围.
的取值范围.
w@w.w.k~s.5*p;m
20、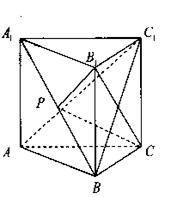 如图,三棱柱ABC-A1B1C1中,侧棱
如图,三棱柱ABC-A1B1C1中,侧棱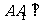 底面AB
底面AB C,
C, 为边长为2的正三角形,点P在A1B上,且AB
为边长为2的正三角形,点P在A1B上,且AB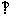 CP。
CP。
(Ⅰ)证明:P为A1B中点;
(Ⅱ)若A1B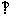 AC1,求二面角B1-PC-B的正弦值。
AC1,求二面角B1-PC-B的正弦值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com