
12.(2010重庆卷)已知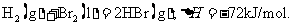 蒸发1mol Br2(l)需要吸收的能量为30kJ,其它相关数据如下表:
蒸发1mol Br2(l)需要吸收的能量为30kJ,其它相关数据如下表:

则表中a为
A.404 B.260 C.230 D.200
22. (本小题满分14分)设曲线C:
(本小题满分14分)设曲线C: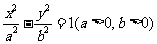 的离心率为
的离心率为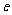 ,右准线
,右准线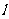
与两渐近线交于P,Q两点,其右焦点为F,且△PQF为等边三角形。
(1)求双曲线C的离心率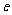 ;
;
(2)若双曲线C被直线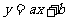 截得弦长为
截得弦长为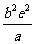 ,求双曲线方程;
,求双曲线方程;
(3)设双曲线C经过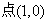 ,以F为左焦点,为
,以F为左焦点,为 左准线的椭圆的短轴端点为B,
左准线的椭圆的短轴端点为B,
求BF 中点的轨迹N方程。
21.(本小题满分12分) 在多面体ABCDE中,AE⊥面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1,F为CD中点.
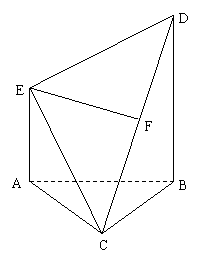 (1)求证:EF⊥面BCD;
(1)求证:EF⊥面BCD;
(2)求面CDE与面ABDE所成的二面角的余弦值.
20.(本小题满分12分)如图,平面直角坐标系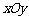 中,
中,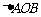 和
和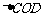 为两等腰直角三角形,
为两等腰直角三角形,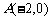 ,C(a,0)(a>0).设
,C(a,0)(a>0).设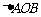 和
和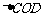 的外接圆圆心分别为
的外接圆圆心分别为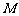 ,
,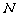 .
.
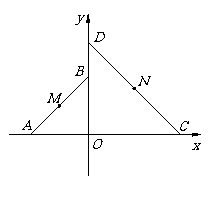 (Ⅰ)若⊙M与直线CD相切,求直线CD的方程;
(Ⅰ)若⊙M与直线CD相切,求直线CD的方程;
(Ⅱ)若直线AB截⊙N所得弦长为4,求⊙N的标准方程;
.
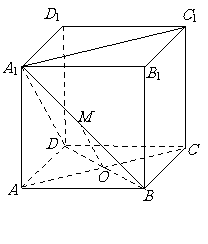
19. (本小题满分12分) 如图,在边长为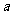 的正方体
的正方体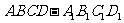 中,
中,
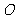 是底面正方形
是底面正方形 的中心,
的中心,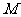 是线段
是线段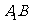 的中点.
的中点.
 (1)证明:
(1)证明: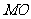 //平面
//平面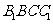 ;
;
(2)求点C1到平面A1DB的距离.
18.(本小题满分12分)盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球. 规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得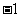 分 . 现从盒内任取3个球.
分 . 现从盒内任取3个球.
(1求取出的3个球颜色互不相同的概率;
(2求取出的3个球得分之和恰为1分的概率;
17.(本小题满分12分)用1,2,3,4,5,6六个数字组成没有重复数字的六位数.
(1) 1,3,5相邻的有多少个数?
(2) 奇数数字,偶数数字相间的有多少个数?
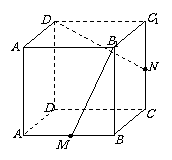
16.如图所示,在正方体ABCD-A1B1C1D1中,M、N分别是棱AB、CC1的中点,△MB1P的顶点P在棱CC1与棱 C1D1上运动,有以下四个命题:
(1).平面MB1P⊥ND1;(2).平面MB1P⊥平面ND1A1;
(3).△MB1P在底面ABCD上的射影图形的面积为定值;
(4).△MB1P在侧面D1C1CD上的射影图形是三角形.
其中正确命题的序号有
15.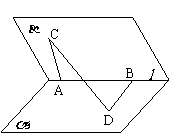 如右图在二面角
如右图在二面角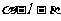 的棱
的棱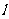 上有
上有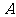 ,
,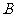 两点,直线
两点,直线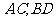 分别在这个二面角的两个半平面内,且都垂直于
分别在这个二面角的两个半平面内,且都垂直于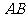 ,若
,若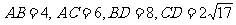 ,则二面角
,则二面角 的大小为
的大小为
14.若双曲线 的一条准线与抛物线y2=4x的准线重合,则双曲线的渐近线方程
的一条准线与抛物线y2=4x的准线重合,则双曲线的渐近线方程
是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com