
2.在复平面内,复数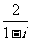 对应的点到直线
对应的点到直线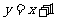 的距离是
.
的距离是
.
1. 集合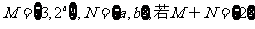 ,则
,则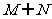 =
.
=
.
21. (本小题满分14分)已知函数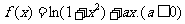 .
.
(Ⅰ)若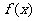 在
在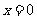 处取得极值,求
处取得极值,求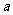 的值;
的值;
(Ⅱ)讨论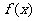 的单调性;
的单调性;
(Ⅲ)证明: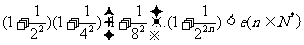 。
。
20.(本小题满分12分)动点P到A(-1,0)及B(1,0)连线的斜率之积为m(m>0)且P的轨迹E的离心率为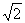 m。
m。
⑴求E的方程; ⑵设直线L: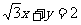 交曲线E于M、N,求ΔAMN的面积。
交曲线E于M、N,求ΔAMN的面积。
19. (本题满分13分)在数列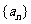 中,
中,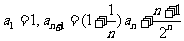
(I)设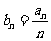 ,求数列
,求数列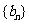 的通项公式;
的通项公式;
(II)求数列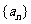 的前
的前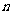 项和
项和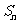 。
。
18. (本题满分12分)如图是某直三棱柱(侧棱与底面垂直)
(本题满分12分)如图是某直三棱柱(侧棱与底面垂直)
被削去上底后的直观图与三视 图的侧视图、俯视图.
在直观图中,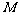 是
是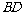 的中点.侧视图是直角梯形,俯视
的中点.侧视图是直角梯形,俯视
图是等腰直角三角形,有关数据如图所示.
(1)求证:EM∥平面ABC;
(2)试问在棱DC上是否存在点N,使NM⊥平面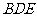 ?
若存在,确定点N的位置;若不存在,请说明理由.
?
若存在,确定点N的位置;若不存在,请说明理由.
(3)求二面角D-EB-A的大小的余弦值.
17. (本题满分12分)在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖。某顾客从此10张券中任抽2张,求:
(1)该顾客中奖的概率;www.
(2)该顾客获得的奖品总价值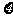 (元)的概率分布列和数学期望。
(元)的概率分布列和数学期望。
16.(本题满分12分)已知向量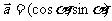 ,
, 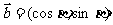 ,
,  .
.
(Ⅰ)求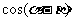 的值;
的值;
(Ⅱ)若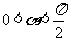 ,
,  , 且
, 且 , 求
, 求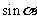 .
.
15. 四位同学在研究函数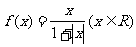 时,分别给出下面四个结论:
①函数
时,分别给出下面四个结论:
①函数 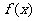 的图象关于
的图象关于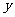 轴对称; ② 函数
轴对称; ② 函数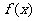 的值域为 (-1,1);
的值域为 (-1,1);
③若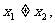 则一定有
则一定有 ;
;
④若规定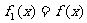 ,
,  ,则
,则 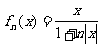 对任意
对任意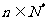 恒成立. 你认为上述四个结论中正确的有
恒成立. 你认为上述四个结论中正确的有
14. 设P为△ABC内一点,若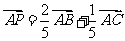 ,则△ABP的面积与△BCP的面积之比为
,则△ABP的面积与△BCP的面积之比为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com