
19.(本小题满分12分)
已知抛物线C: 过点A (1 , -2)。
过点A (1 , -2)。
(I)求抛物线C 的方程,并求其准线方程;
(II)是否存在平行于OA(O为坐标原点)的直线L,使得直线L与抛物线C有公共点,且直线OA与L的距离等于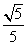 ?若存在,求直线L的方程;若不存在,说明理由。
?若存在,求直线L的方程;若不存在,说明理由。

18.(本小题满分12分)
设平顶向量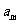 = ( m , 1),
= ( m , 1), 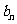 = ( 2 , n ),其中 m, n
= ( 2 , n ),其中 m, n  {1,2,3,4}.
{1,2,3,4}.
(I)请列出有序数组( m,n )的所有可能结果;
(II)记“使得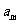
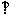 (
(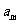 -
-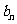 )成立的( m,n )”为事件A,求事件A发生的概率。
)成立的( m,n )”为事件A,求事件A发生的概率。

17. (本小题满分12分 )
数列{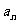 } 中
} 中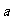 =
=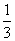 ,前n项和
,前n项和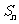 满足
满足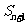 -
-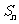 =
=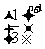 (n
(n
 ).
).
( I ) 求数列{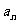 }的通项公式
}的通项公式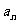 以及前n项和
以及前n项和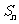 ;
;
(II)若S1, t ( S1+S2 ), 3( S2+S3 ) 成等差数列,求实数t的值。

16. 观察下列等式:
① cos2a=2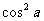 -1;
-1;
② cos4a=8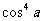 - 8
- 8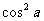 + 1;
+ 1;
③ cos6a=32 - 48
- 48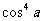 + 18
+ 18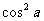 - 1;
- 1;
④ cos8a=128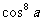 - 256
- 256 + 160
+ 160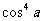 - 32
- 32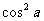 + 1;
+ 1;
⑤ cos10a=
m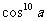 - 1280
- 1280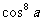 + 1120
+ 1120 + n
+ n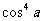 + p
+ p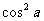 - 1.
- 1.
可以推测,m – n + p= .
[答案]962
[解析]因为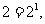
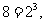
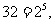
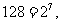 所以
所以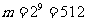 ;观察可得
;观察可得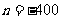 ,
,
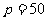 ,所以m – n +p =962。
,所以m – n +p =962。
[命题意图]本小题考查三角变换、类比推理等基础知识,考查同学们的推理能力等。
15. 对于平面上的点集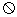 ,如果连接
,如果连接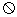 中任意两点的线段必定包含于
中任意两点的线段必定包含于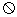 ,则称
,则称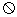 为平面上的凸集,给出平面上4个点集的图形如下(阴影区域及其边界):
为平面上的凸集,给出平面上4个点集的图形如下(阴影区域及其边界):

其中为凸集的是 (写出所有凸集相应图形的序号)。
[答案]②③
[解析]
[命题意图]
14. 将容量为n的样本中的数据分成6组,绘制频率分布直方图。若第一组至第六组数据的频率之比为2:3:4:6:4:1,且前三组数据的频数之和等于27,则n等于 。
[答案]60
[解析]设第一组至第六组数据的频率分别为 ,则
,则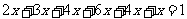 ,解得
,解得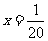 ,所以前三组数据的频率分别是
,所以前三组数据的频率分别是 ,
,
故前三组数据的频数之和等于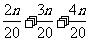 =27,解得n=60。
=27,解得n=60。
[命题意图]本小题考查频率分布直方图的基础知识,熟练基本公式是解答好本题的关键。
13. 若双曲线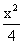 -
-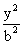 =1(b>0)的渐近线方程式为y=
=1(b>0)的渐近线方程式为y= ,则b等于 。
,则b等于 。
[答案]1
[解析]由题意知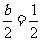 ,解得b=1。
,解得b=1。
[命题意图]本小题考查双曲线的几何性质、待定系数法,属基础题。
12.设非空集合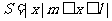 满足:当
满足:当 时,有
时,有 。给出如下三个命题工:①若
。给出如下三个命题工:①若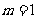 ,则
,则 ;②若
;②若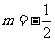 ,则
,则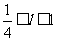 ;③若
;③若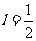 ,则
,则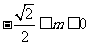 。其中正确命题的个数是
。其中正确命题的个数是
A.0 B.1 C.2 D.3
[答案]D
[解析]
[命题意图]
第II卷(非选择题,共90分)
11.若点O和点F分别为椭圆 的中心和左焦点,点P为椭圆上的任意一点,则
的中心和左焦点,点P为椭圆上的任意一点,则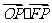 的最大值为
的最大值为
A.2 B.3 C.6 D.8
[答案]C
[解析]由题意,F(-1,0),设点P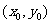 ,则有
,则有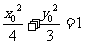 ,解得
,解得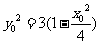 ,
,
因为 ,
, ,所以
,所以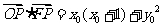
=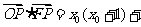
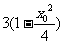 =
= ,此二次函数对应的抛物线的对称轴为
,此二次函数对应的抛物线的对称轴为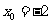 ,因为
,因为 ,所以当
,所以当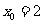 时,
时,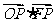 取得最大值
取得最大值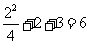 ,选C。
,选C。
[命题意图]本题考查椭圆的方程、几何性质、平面向量的数量积的坐标运算、二次函数的单调性与最值等,考查了同学们对基础知识的熟练程序以及知识的综合应用能力、运算能力。
7.函数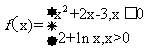 的零点个数为 ( )
的零点个数为 ( )
A.3 B.2 C.1 D.0
[答案]B
[解析]当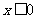 时,令
时,令 解得
解得 ;
;
当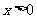 时,令
时,令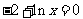 解得
解得 ,所以已知函数有两个零点,选C。
,所以已知函数有两个零点,选C。
[命题意图]本题考查分段函数零点的求法,考查了分类讨论的数学思想。

[命题意图]本题考查三角函数的周期、图象变换等基础知识。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com