
23.选修4-4:坐标系与参数方程
已知曲线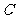 的极坐标方程为
的极坐标方程为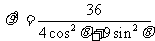 ;
;
(1)若以极点为原点,极轴所在的直线为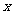 轴,求曲线
轴,求曲线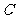 的直角坐标方程;
的直角坐标方程;
(2)若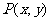 是曲线
是曲线 上的一个动点,求
上的一个动点,求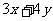 的最大值
的最大值
22.选修4-1:几何证明选讲
如图,PA切圆O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转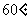 到O D.
到O D.
(1)求线段PD的长;
(2)在如图所示的图形中是否有长度为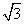 的线段?若有,指出该线段;若没有,说明理由.
的线段?若有,指出该线段;若没有,说明理由.

21.(本小题满分12分)已知函数f (x) = ln (2 + 3x) 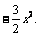
(1)求f (x)在[0,1]上的最大值;
(2)若对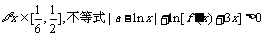 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若关于x的方程f (x) = –2x + b在[0,1]上恰有两个不同的实根,求实数b的取值范围.
请考生在第22,23,24三题中任选一题做答,如果多做,则按所做的第一题计分。(本小题满分10分)
20.(本小题满分12分)
已知中心在原点,焦点在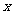 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为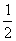 ,且经过点
,且经过点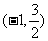 ,过点P(2,1)的直线
,过点P(2,1)的直线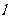 与椭圆C在第一象限相切于点M .
与椭圆C在第一象限相切于点M .
(1)求椭圆C的方程;
(2)求直线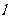 的方程以及点M的坐标;
的方程以及点M的坐标;
(3) 是否存过点P的直线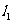 与椭圆C相交于不同的两点A、B,满足
与椭圆C相交于不同的两点A、B,满足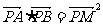 ?若存在,求出直线l1的方程;若不存在,请说明理由.
?若存在,求出直线l1的方程;若不存在,请说明理由.
19.(本小题满分12分)
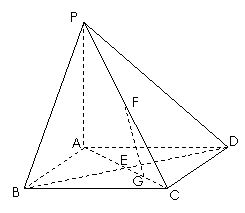
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由.
(3)当二面角B-PC-D的大小为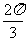 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
18.某市十所重点中学进行高三联考,共有5000名考生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在这次测试中的数学成绩,制成如下频率分布表:
(1)根据上面的频率分布表,求①,②,③,④处的数值;
(2)根据上面的频率分布表,在所给的坐标系中画出在区间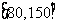 上的频率分布直方图;
上的频率分布直方图;
(3)如果把表中的频率近似地看作每个学生在这次考试中取得相应成绩的概率,那么从总体中任意抽取3个个体,成绩落在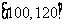 中的个体数为
中的个体数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
|
分组 |
频数 |
频率 |
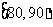 |
① |
② |
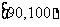 |
|
0.050 |
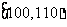 |
|
0.200 |
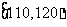 |
36 |
0.300 |
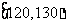 |
|
0.275 |
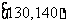 |
12 |
③ |
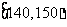 |
|
0.050 |
|
合计 |
④ |
|
17.(本小题满分12分)
在△ABC中,a,b,c分别是角A,B,C的对边,A为锐角,已知向量
(1)若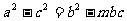 ,求实数m的值。
,求实数m的值。
(2)若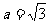 ,求△ABC面积的最大值.
,求△ABC面积的最大值.
16.有下列命题:
①若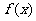 存在导函数,则
存在导函数,则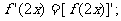
②若函数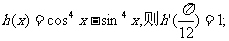
③若函数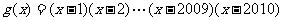 ,则
,则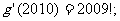
④若三次函数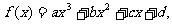 则
则 是“
是“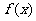 有极值点”的充要条件.
有极值点”的充要条件.
其中真命题的序号是_________.
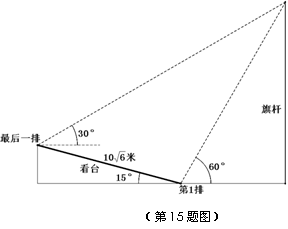
15.某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15°的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,且第一排和最后一排的距离为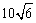 米(如图所示),旗杆底部与第一排在一个水平面上.若国歌长度约为50秒,升旗手应以_________(米/秒)的速度匀速升旗.
米(如图所示),旗杆底部与第一排在一个水平面上.若国歌长度约为50秒,升旗手应以_________(米/秒)的速度匀速升旗.
14.若实数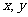 满足不等式组
满足不等式组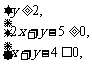 则
则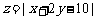 的最小值是________.
的最小值是________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com