
8.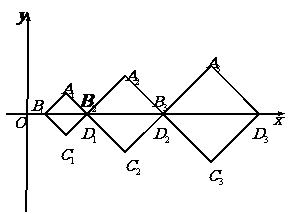 如图,在直角坐标系
如图,在直角坐标系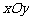 中,有一组对角线长为
中,有一组对角线长为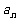 的
的
正方形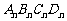
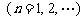 ,其对角线
,其对角线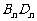 依次放置在
依次放置在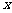 轴上(相邻顶点重合). 设
轴上(相邻顶点重合). 设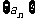 是首项为
是首项为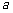 ,公差为
,公差为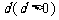 的等差数列,点
的等差数列,点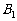 的坐标为
的坐标为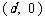 .
.
⑴当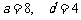 时,证明:顶点
时,证明:顶点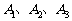 不在同一条直线上;
不在同一条直线上;
⑵在⑴的条件下,证明:所有顶点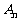 均落在抛物线
均落在抛物线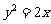 上;
上;
⑶为使所有顶点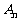 均落在抛物线
均落在抛物线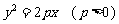 上,求
上,求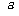 与
与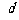 之间所应满足的关系式.
之间所应满足的关系式.
7.我们将具有下列性质的所有函数组成集合M:函数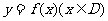 ,对任意
,对任意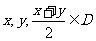 均满足
均满足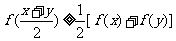 ,当且仅当
,当且仅当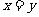 时等号成立.
时等号成立.
⑴若定义在(0,+∞)上的函数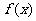 ∈M,试比较
∈M,试比较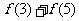 与
与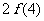 大小.
大小.
⑵给定两个函数: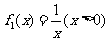 ,
,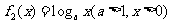 .
.
证明: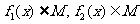 .
.
⑶
试利用⑵的结论解决下列问题:若实数m、n满足 ,求m+n的最大值.
,求m+n的最大值.
6.设数列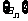 的前n项和为
的前n项和为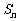 ,已知
,已知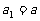 (
(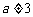 ),
),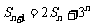 ,
,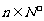 .
.
⑴设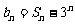 ,
,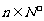 ,证明数列
,证明数列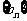 为等比数列;
为等比数列;
⑵求数列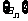 的通项公式;
的通项公式;
⑶若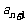 ≥
≥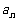 ,
,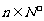 ,求a的取值范围.
,求a的取值范围.
5.已知a,b是非零实常数,函数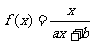 满足
满足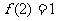 ,且方程
,且方程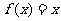 有且仅有一个解。
有且仅有一个解。
(1)求a,b的值;
(2)是否存在实常数m,使得对于定义域中任意的x,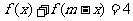 恒成立?为什么?
恒成立?为什么?
(3)在直角坐标系中,若把函数 的图象向右平移
的图象向右平移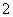 个单位,得到函数
个单位,得到函数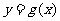 的图象。试求
的图象。试求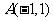 到函数
到函数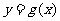 图象上任意一点
图象上任意一点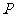 的距离
的距离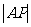 的最小值。
的最小值。
4.已知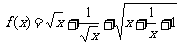 及
及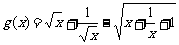 .
.
(1)求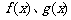 的定义域及
的定义域及 的值;
的值;
(2)求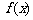 的最小值;
的最小值;
(3)若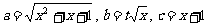 ,是否存在满足下列条件的正数
,是否存在满足下列条件的正数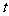 ,使得对于任意的正数
,使得对于任意的正数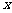 ,
,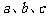 都可以成为某个三角形三边的长?若存在,则求出
都可以成为某个三角形三边的长?若存在,则求出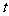 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
3.已知,数列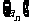 有
有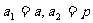 (常数
(常数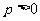 ),对任意的正整数
),对任意的正整数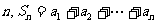 ,并有
,并有 满足
满足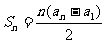 。(1)求
。(1)求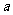 的值;
的值;
(2)试确定数列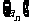 是不是等差数列,若是,求出其通项公式。若不是,说明理由;
是不是等差数列,若是,求出其通项公式。若不是,说明理由;
(3)对于数列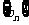 ,假如存在一个常数
,假如存在一个常数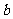 使得对任意的正整数
使得对任意的正整数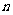 都有
都有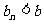 且
且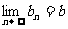 ,则称
,则称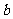 为数列
为数列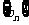 的“上渐进值”,令
的“上渐进值”,令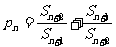 ,求数列
,求数列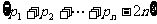 的“上渐进值”。
的“上渐进值”。
2.在△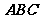 中,已知
中,已知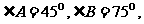 点
点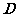 在
在
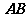 上,且
上,且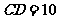 .(1)若点
.(1)若点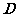 与点
与点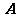 重合,试求线段
重合,试求线段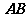 的长;
的长;
(2)在下列各题中,任选一题,并写出计算过程,求出结果.
①(解答本题,最多可得6分)若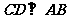 ,求线段
,求线段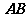 的长;
的长;
②(解答本题,最多可得8分)若 平分
平分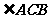 ,求线段
,求线段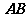 的长;
的长;
③(解答本题,最多可得10分)若点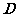 为线段
为线段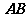 的中点,求线段
的中点,求线段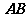 的长.
的长.
1. 在某个旅游业为主的地区,每年各个月份从事旅游服务工作的人数会发生周期性的变化. 现假设该地区每年各个月份从事旅游服务工作的人数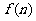 可近似地用函数
可近似地用函数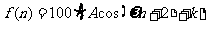 来刻画. 其中:正整数
来刻画. 其中:正整数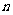 表示月份且
表示月份且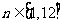 ,例如
,例如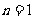 时表示1月份;
时表示1月份;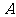 和
和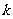 是正整数;
是正整数; .
.
统计发现,该地区每年各个月份从事旅游服务工作的人数有以下规律:
① 各年相同的月份,该地区从事旅游服务工作的人数基本相同;
② 该地区从事旅游服务工作的人数最多的8月份和最少的2月份相差约400人;
③ 2月份该地区从事旅游服务工作的人数约为100人,随后逐月递增直到8月份达到最多.
⑴
试根据已知信息,确定一个符合条件的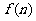 的表达式;
的表达式;
⑵一般地,当该地区从事旅游服务工作的人数超过400人时,该地区也进入了一年中的旅游“旺季”. 那么,一年中的哪几个月是该地区的旅游“旺季”?请说明理由.
25.(10分)黄铜(由锌和铜形成的合金)有较强的耐磨性能,在生活中有广泛的用途。晓军同学为了测定黄铜屑样品组成,分四次取样品与稀硫酸反应,其实验数据记录如下表:
|
|
1 |
2 |
3 |
4 |
|
样品质量/g |
25.0 |
25.0 |
25.0 |
30.0 |
|
稀硫酸质量/g |
80 |
100 |
120 |
100 |
|
产生气体质量/g |
0.4 |
0.5 |
0.5 |
0.5 |
计算:
(1)第 次实验样品与稀硫酸恰好完全反应。
(2)黄铜样品中铜的质量分数是 。
(3)所用稀硫酸中溶质质量分数,写出计算过程。
24.(7分)儿童缺锌会引起食欲不振、发育不良。右图为某种补锌口服液说明书的一部分,请回答:
(1)该口服液中的锌属于 (填:“常量”或“微量”)元素;
葡萄糖酸锌分子中的碳、氢元素的质量比为 。
(2)每支口服液中锌的质量分数为 (1g=1000mg)。
(3)若儿童1kg体重每日需要0.5mg锌,每天从食物中只能摄入所需锌的一半;体重为20kg的儿童每天还须服该口服液 支,才能满足身体的需要.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com