
2.某几何体的三视图如下图所示,则该几何体是

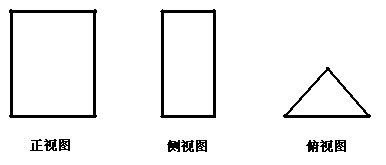
A.圆柱 B.圆锥 C.三棱柱 D.三棱锥
1.设集合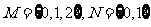 ,则
,则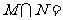
A. B.
B.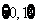 C.
C.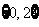 D.
D.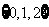
[例1]函数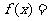
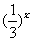 在区间
在区间 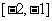 上的最大值是
上的最大值是
A.1 B.9 C. 27 D.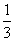
说明:此题属于容易题,考查指数函数的单调性和最值,可以通过图形判断最大值.
[例2]在编制将两变量a,b的数值交换的正确的程序中,必须使用到的语句是
A.输入、输出语句 B. 输入、输出语句,条件语句
C.输入、输出语句,赋值语句 D. 输入、输出语句,循环语句
说明:此题属于容易题,考查基本算法语句的应用.
[例3]已知在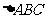 中,
中,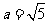 ,
,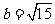 ,
,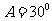 ,则
,则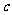 等于
等于
A.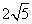 B.
B.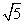 或
或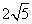 C.
C.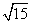 D.以上都不对
D.以上都不对
说明:此题属于中档题,考查正弦定理、余弦定理的应用.
[例4]不等式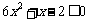 的解集是
的解集是
A.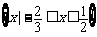 B .
B .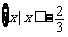 ,或
,或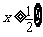
C.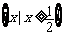 D.
D.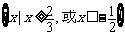
说明:此题属于容易题,考查一元二次不等式的解法.
[例5]某中学有高级教师28人,中级教师54人,初级教师81人,为了调查他们的身体状况,从他们中抽取容量为36的样本,最适合抽取样本的方法是
A.简单随机抽样 B.系统抽样
C.分层抽样 D.先从高级教师中随机剔除1人,再用分层抽样
说明:此题属于容易题,考查统计的有关知识.
[例6]已知两个不同平面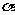 、
、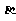 ,如果平面
,如果平面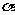 内的两条相交直线m,n都和直线b垂直,且b⊥
内的两条相交直线m,n都和直线b垂直,且b⊥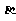 ,则平面
,则平面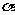 与
与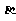 的关系是 .
的关系是 .
说明:此题属于容易题, 考查线线垂直、线面垂直、面面平行的定理的应用.
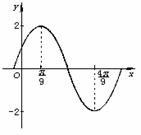 [例7]如图,已知函数y=Asin(ωx+
[例7]如图,已知函数y=Asin(ωx+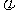 ),在同一周期内,当x=
),在同一周期内,当x=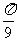 时函数取得最大值2,当x=
时函数取得最大值2,当x=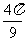 时函数取得最小值-2,则该函数的解析式为_______________.
时函数取得最小值-2,则该函数的解析式为_______________.
说明:此题属于中档题,考查三角函数的图像与性质.
[例8]已知数列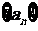 的前n项和为
的前n项和为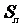 ,
,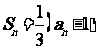
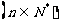
⑴ 求 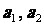 ; ⑵ 求证:数列
; ⑵ 求证:数列 是等比数列.K^S*5U.C#O
是等比数列.K^S*5U.C#O
说明:此题属于中档题,考查等比数列的通项公式及前n项和公式的应用.
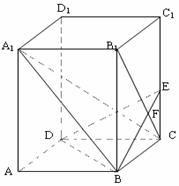 [例9]已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1=4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
[例9]已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1=4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
(1)求截面BDE分正四棱柱ABCD-A1B1C1D1两部
分体积比;
(2)求证:A1C⊥BE.
说明: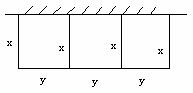 此题属于稍难题,考查空间线面的位置关系和三棱锥体积的求法等。
此题属于稍难题,考查空间线面的位置关系和三棱锥体积的求法等。
[例10]有一批材料可以建成长为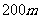 的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图),则围成的矩形的最大面积是多少?
的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图),则围成的矩形的最大面积是多少?
说明:此题属于稍难题,考查数学建模能力.
[例11]已知圆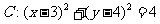 ,直线
,直线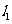 过定点A(1,0).
过定点A(1,0).
(Ⅰ)若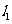 与圆相切,求
与圆相切,求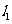 的方程;
的方程;
(Ⅱ)若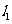 与圆相交于P,Q两点,线段PQ的中点为M,又
与圆相交于P,Q两点,线段PQ的中点为M,又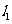 与
与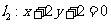 的交点为N,求证:
的交点为N,求证: 为定值.
为定值.
说明:此题属于稍难题,考查直线和圆的位置关系及用代数方法处理几何问题的思想.
试卷包含选择题、填空题和解答题三种题型。其中选择题是四选一型的单项选择题;填空题只要求直接写出结果,不必写出计算过程或推证过程;解答题包括计算题、证明题和应用题等。解答应写出文字说明、演算步骤或推理论证过程。三种题型所占分数的百分比约为:选择题占45%,填空题占15%,解答题占40%。K^S*5U.C#O
试题按其难度分为容易题,中档题和稍难题。其中难度值为0.8以上的试题为容易题,约占80%;难度值为0.6-0.8之间的试题为中档题,约占10%;难度值为0.4-0.6之间的试题为较难题,约占10%;不出现难度值为0.3以下的试题。试卷的总体难度控制在0.8左右。
考试采用闭卷笔试的形式,全卷100分,考试时间90分钟。
(三)不等式
1.不等关系与一元二次不等式
了解不等式(组)的实际背景,会从实际问题的情境中抽象出不等式模型;了解一元二次不等式与相应的二次函数、一元二次方程的联系;会解一元二次不等式。
2.二元一次不等式组与简单线性规划问题
会从实际情境中抽象出二元一次不等式组;了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组;会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决。
3.基本不等式: 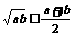 (a,b≥0)
(a,b≥0)
了解基本不等式的证明过程;会用基本不等式解决简单的最大(小)值问题。
(二)数列
1.数列的概念和简单表示法
了解数列的概念和几种简单的表示方法(列表、图象、通项公式);知道数列是自变量为正整数的特殊函数。
2.等差数列、等比数列
理解等差数列、等比数列的概念;掌握等差数列、等比数列的通项公式与前n项和公式;能判断数列的等差或等比关系,并用等差数列、等比数列的有关知识解决相应的问题;了解等差数列与一次函数的关系,等比数列与指数函数的关系。
(一)解三角形
1.正弦定理和余弦定理
掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题。
2.正弦定理和余弦定理的应用
能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题。
(十)三角恒等变换
1.两角和与差的三角函数公式
会用向量的数量积推导出两角差的余弦公式;会用两角差的余弦公式推导出两角和的正弦、余弦、正切公式,二倍角的正弦、余弦、正切公式,了解它们的内在联系。
2.简单的三角恒等变换
能运用上述公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式,但不要求记忆)。
(九)平面向量
1.平面向量的实际背景及基本概念
了解向量的实际背景;理解平面向量概念和两个向量相等的含义;理解向量的几何表示。
2.向量的线性运算
掌握向量加、减法的运算,理解其几何意义;掌握向量数乘运算及其几何意义,理解两个向量共线的含义;了解向量的线性运算性质及其几何意义。
3.平面向量的基本定理及坐标表示
了解平面向量的基本定理及其意义;掌握平面向量的正交分解及其坐标表示;会用坐标表示平面向量的加法、减法与数乘运算;理解用坐标表示的平面向量共线的条件。
4.平面向量的数量积
理解平面向量数量积的含义及其物理意义;了解平面向量的数量积与向量投影的关系;掌握数量积的坐标表达式,会进行平面向量数量积的运算;会运用数量积表示两个向量的夹角,会判断两个平面向量的垂直关系。
5.向量的应用
会用向量方法解决一些简单的平面几何问题;会用向量方法解决简单的力学问题与其他一些实际问题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com