
5.B [命题意图]本小题主要考查了考生对二项式定理的掌握情况,尤其是展开式的通项公式的灵活应用,以及能否区分展开式中项的系数与其二项式系数,同时也考查了考生的一些基本运算能力.
[解析]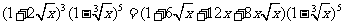
故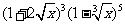 的展开式中含x的项为
的展开式中含x的项为 ,所以x的系数为-2.
,所以x的系数为-2.
(6)某校开设A类选修课3门,B类选择课4门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有
(A) 30种 (B)35种 (C)42种 (D)48种
4.A[命题意图]本小题主要考查等比数列的性质、指数幂的运算、根式与指数式的互化等知识,着重考查了转化与化归的数学思想.
[解析]由等比数列的性质知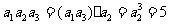 ,
,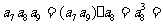 10,所以
10,所以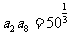 ,
,
所以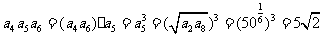
(5)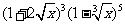 的展开式中x的系数是
的展开式中x的系数是
(A) -4 (B) -2 (C) 2 (D) 4
3.B [命题意图]本小题主要考查线性规划知识、作图、识图能力及计算能力.
[解析]画出可行域(如右图),由图可知,当直线 经过点A(1,-1)时,z最大,且最大值为
经过点A(1,-1)时,z最大,且最大值为 .
.


(4)已知各项均为正数的等比数列{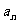 },
},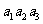 =5,
=5,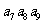 =10,则
=10,则
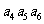 =
=
(A) 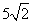 (B) 7 (C) 6 (D)
(B) 7 (C) 6 (D) 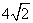
2.B [命题意图]本小题主要考查诱导公式、同角三角函数关系式等三角函数知识,并突出了弦切互化这一转化思想的应用.
[解析]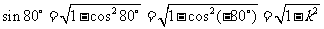 ,所以
,所以
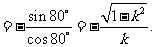
(3)若变量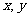 满足约束条件
满足约束条件 则
则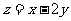 的最大值为
的最大值为
(A)4 (B)3 (C)2 (D)1
(1)复数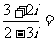
(A)i (B) (C)12-13
(C)12-13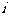 (D) 12+13
(D) 12+13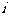
1.A[命题意图]本小题主要考查复数的基本运算,重点考查分母实数化的转化技巧.
[解析]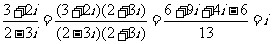 .
.
(2)记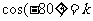 ,那么
,那么
A.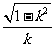 B. -
B. -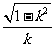 C.
C.  D. -
D. -
(16)(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分. )
已知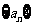 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,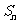 为
为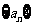 的前
的前 项和.
项和.
(Ⅰ)求通项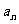 及
及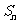 ;
;
(Ⅱ)设 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列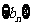 的通项公
的通项公 式及其前
式及其前 项和
项和 .
.
(17)(本小题满分13分 ,(Ⅰ)小问6分,(Ⅱ)小问7分. )
,(Ⅰ)小问6分,(Ⅱ)小问7分. )
在甲、乙等6个单位参加的一次“唱读讲传”演出活动中,每个单位的 节目集中安排在一起. 若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,……,6),求:
节目集中安排在一起. 若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,……,6),求:
(Ⅰ)甲、乙两单位的演出序号均为偶数的概率;
(Ⅱ)甲、乙两单位的演出序号不相邻的概率.
(18).(本小题满分13分), (Ⅰ)小问5分,(Ⅱ)小问8分.)
设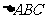 的内角A、B、C的对边长分别为a、b、c,且3
的内角A、B、C的对边长分别为a、b、c,且3 +3
+3
 -3
-3 =4
=4 bc .
bc .
(Ⅰ) 求s inA的值;
inA的值;
(Ⅱ)求 的值.
的值.
(19) (本小题满分12分), (Ⅰ)小问5分,(Ⅱ)小问7分.)
已知 函数
函数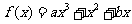 (其中常数a,b∈R),
(其中常数a,b∈R),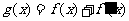 是奇函数.
是奇函数.
(Ⅰ)求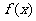 的表达式;
的表达式;
(Ⅱ)讨论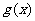 的单调性,并求
的单调性,并求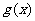 在区间[1,2]上的最大值和最小值.
在区间[1,2]上的最大值和最小值.
(20)(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分. )
如题(20)图,四棱锥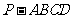 中,底面
中,底面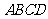 为矩形,
为矩形, 底面
底面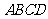 ,
,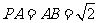 ,点
,点 是棱
是棱 的中点.
的中点.
(Ⅰ)证明: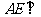 平面
平面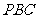 ;
;
(Ⅱ)若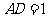 ,求二面角
,求二面角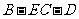 的平面角的余弦值.
的平面角的余弦值.
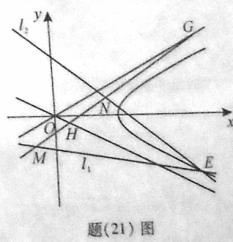 (21)(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分. )
(21)(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分. )
已知以原点 为中心,
为中心, 为右焦点的双曲线
为右焦点的双曲线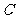 的离心率
的离心率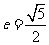 .
.
(Ⅰ)求双曲线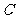 的标准方程及其渐近线方程;
的标准方程及其渐近线方程;
(Ⅱ)如题(21)图,已知过点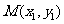 的直线
的直线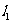 :
: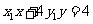 与过点
与过点 (其中
(其中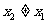 )的直线
)的直线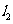 :
: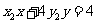 的交点
的交点 在双曲线
在双曲线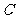 上,直线
上,直线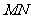 与双曲线的两条
与双曲线的两条 渐近线分别交于
渐近线分别交于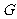 、
、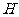 两点,求
两点,求 的值.
的值.
(11)设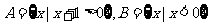 ,则
,则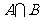 =____________ .
=____________ .
(12)已知 ,则函数
,则函数 的最小值为____________ .
的最小值为____________ .
 (13)已知过抛物线
(13)已知过抛物线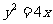 的焦点
的焦点 的直线交该抛物线于
的直线交该抛物线于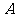 、
、 两点,
两点,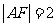 ,则
,则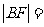 ____________ .
____________ .
(14)加工某一零件需经过三道工序,设第一、二、三道工序的次品率分别为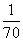 、
、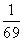 、
、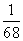 ,且各道工序互不影响,则加工出来的零件的次品率为____________
.
,且各道工序互不影响,则加工出来的零件的次品率为____________
.
(15)如 题(15)图,图中的实线是由三段圆弧连接而成的一条
题(15)图,图中的实线是由三段圆弧连接而成的一条 封闭曲线
封闭曲线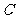 ,各段弧所在的圆经过同一点
,各段弧所在的圆经过同一点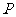 (点
(点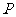 不在
不在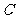 上)且半径相等. 设第
上)且半径相等. 设第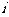 段弧所对的圆心角为
段弧所对的圆心角为 ,则
,则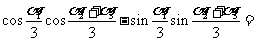 ____________ .
____________ .
(1)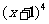 的展开式中
的展开式中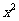 的系数为
的系数为
(A)4 (B)6
(C)10 (D)20
(2)在等差数列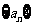 中,
中,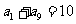 ,则
,则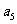 的值为
的值为
(A)5 (B)6
(C)8 (D)10
(3)若向量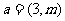 ,
,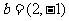 ,
,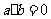 ,则实数
,则实数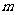 的值为
的值为
(A)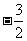 (B)
(B)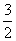
(C)2 (D)6
(4)函数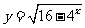 的值域是
的值域是
(A) (B)
(B)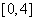
(C)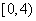
 (D)
(D)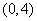
(5)某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本 . 若样本中的青年职工为7人,则样本容量为
(A)7  (B)15
(B)15
(C)25 (D)35
(6)下列函数中,周期为 ,且在
,且在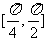 上为减函数的是
上为减函数的是
(A)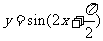 (B)
(B)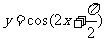
(C)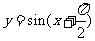 (D)
(D)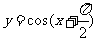
(7)设变量 满足约束条件
满足约束条件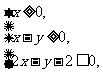 则
则 的最大值为
的最大值为
(A)0 (B)2
(C)4 (D)6
(8)若直线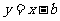 与曲线
与曲线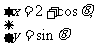 (
(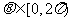 )有两个不同的公共点,则实数
)有两个不同的公共点,则实数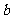 的取值范围为
的取值范围为
(A)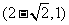 (B)
(B)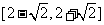
(C)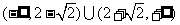 (D)
(D)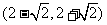
(9)到两互相垂直的异面直线的距离相等的点
(A)只 有1个
(B)恰有3个
有1个
(B)恰有3个
 (C)恰有4个
(D)有无穷多个
(C)恰有4个
(D)有无穷多个
(10)某单位拟 安排6位员工在今年6月14日至16日(端午节假期)值班,每天安排2人,每人值班1天 . 若6位员工中的甲不值14日,乙不值16日,则不同的安排方法共有
安排6位员工在今年6月14日至16日(端午节假期)值班,每天安排2人,每人值班1天 . 若6位员工中的甲不值14日,乙不值16日,则不同的安排方法共有
(A)30种  (B)36种
(B)36种
(C)42种 (D)48种
22.(1)解:把A(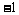 ,0),C(3,
,0),C(3,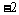 )代入抛物线
)代入抛物线 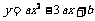 得
得
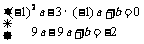 整理得
整理得
 解得
解得
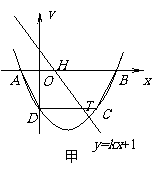 ∴抛物线的表达式为
∴抛物线的表达式为 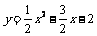
(2)令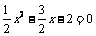 解得
解得 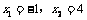
∴ B点坐标为(4,0) 又∵D点坐标为(0,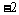 )
)
∴AB∥CD ∴四边形ABCD是梯形.
∴S梯形ABCD =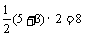
设直线 与x轴的交点为H,
与CD的交点为T,
与x轴的交点为H,
与CD的交点为T,
则H(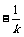 ,0), T(
,0), T( ,
,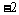 )
∵直线
)
∵直线 将四边形ABCD面积二等分
将四边形ABCD面积二等分
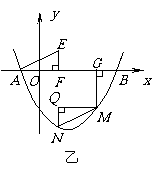 ∴S梯形AHTD =
∴S梯形AHTD =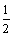 S梯形ABCD=4
∴
S梯形ABCD=4
∴ ∴
∴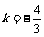
(3)∵MG⊥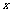 轴于点G,线段MG︰AG=1︰2
轴于点G,线段MG︰AG=1︰2
∴设M(m,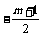 ),
∵点M在抛物线上
),
∵点M在抛物线上
∴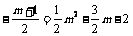 解得
解得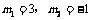 (舍去)
(舍去)
∴M点坐标为(3,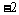 )
)
根据中心对称图形性质知,MQ∥AF,MQ=AF,NQ=EF,
∴N点坐标为(1,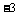 )
)
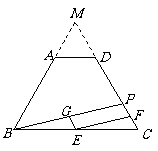
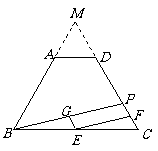
21.解:(1)四边形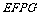 是平行四边形. 理由:∵点
是平行四边形. 理由:∵点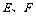 分别是
分别是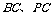 的中点,
的中点,
 ∴
∴ . 同理可证
. 同理可证 .∴四边形
.∴四边形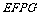 是平行四边形.
是平行四边形.
(2)方法一:当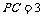 时,四边形
时,四边形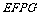 是矩形.
是矩形.
证明:延长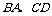 交于点
交于点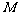 .∵
.∵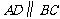 ,
,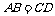 ,
,
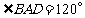 ,∴
,∴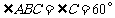 .∴
.∴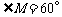 ,
,
∴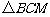 是等边三角形. ∵
是等边三角形. ∵ ,
,
∴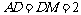 .∴
.∴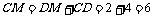 . ∵
. ∵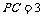 ,
,
∴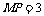 ,∴
,∴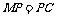 ,∴
,∴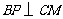 即
即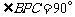 .
.
由(1)可知,四边形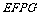 是平行四边形,
是平行四边形,
∴四边形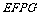 是矩形.方法二:当
是矩形.方法二:当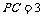 时,四边形
时,四边形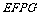 是矩形.
是矩形.
证明:延长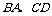 交于点
交于点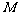 .由(1)可知,四边形
.由(1)可知,四边形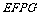 是平行四边形.
是平行四边形.
 当四边形
当四边形 是矩形时,
是矩形时, .∵
.∵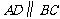 ,
,
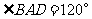 ,∴
,∴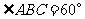 .∵
.∵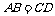 ,
,
∴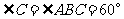 .∴
.∴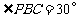 且
且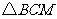 是等边三角形.
是等边三角形.
∴ ,∴
,∴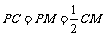 .
.
同方法一,可得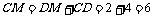 ,∴
,∴ .
.
即当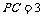 时,四边形
时,四边形 是矩形.
是矩形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com