
5、函数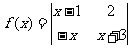 图像的顶点是
图像的顶点是 ,且
,且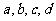 成
成
等比数列,则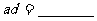
4、执行右边的程序框图,若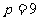 ,则输出的S
,则输出的S
3、
2、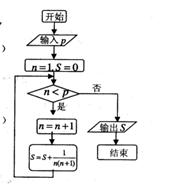 若函数
若函数 的反函数的图像过点
的反函数的图像过点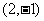 ,则
,则
个空格填对得4分,否则一律得零分)
1、设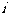 为虚数单位,则复数
为虚数单位,则复数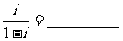

18. [命题意图]本题主要考查等可能性事件、互斥事件、独立事件、相互独立试验、分布列、数学期望等知识,以及运用概率知识解决实际问题的能力,考查分类与整合思想、化归与转化思想.
(19)(本小题满分12分)(注意:在试题卷上作答无效)
如图,四棱锥S-ABCD中,SD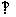 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD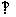 DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC
DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC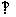 平面SBC .
平面SBC .
(Ⅰ)证明:SE=2EB;
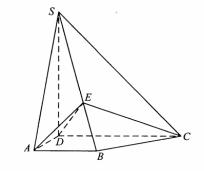 (Ⅱ)求二面角A-DE-C的大小 .
(Ⅱ)求二面角A-DE-C的大小 .
[命题意图]本小题主要考查空间直线与直线、直线与平面、平面与平面的位置关系,二面角等基础知识,考查空间想象能力、推理论证能力和运算能力.
(20)(本小题满分12分)(注意:在试题卷上作答无效)
已知函数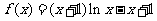 .
.
(Ⅰ)若 ,求
,求 的取值范围;
的取值范围;
(Ⅱ)证明: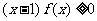 .
.
[命题意图]本小题主要考查函数、导数、不等式证明等知识,通过运用导数知识解决函数、不等式问题,考查了考生综合运用数学知识解决问题的能力以及计算能力,同时也考查了函数与方程思想、化归与转化思想.
(21)(本小题满分12分)(注意:在试题卷上作答无效)
已知抛物线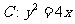 的焦点为F,过点
的焦点为F,过点 的直线
的直线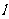 与
与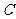 相交于
相交于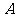 、
、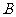 两点,点A关于
两点,点A关于 轴的对称点为D .
轴的对称点为D .
(Ⅰ)证明:点F在直线BD上;
(Ⅱ)设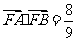 ,求
,求 的内切圆M的方程 .
的内切圆M的方程 .
[命题意图]本小题为解析几何与平面向量综合的问题,主要考查抛物线的性质、直线与圆的位置关系,直线与抛物线的位置关系、圆的几何性质与圆的方程的求解、平面向量的数量积等知识,考查考生综合运用数学知识进行推理论证的能力、运算能力和解决问题的能力,同时考查了数形结合思想、设而不求思想..
(22)(本小题满分12分)(注意:在试题卷上作答无效)
已知数列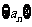 中,
中,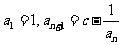 .
.
(Ⅰ)设 ,求数列
,求数列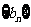 的通项公式;
的通项公式;
(Ⅱ)求使不等式 成立的
成立的 的取值范围 .
的取值范围 .
[命题意图]本小题主要考查数列的通项公式、等比数列的定义、递推数列、不等式等基础知识和基本技能,同时考查分析、归纳、探究和推理论证问题的能力,在解题过程中也渗透了对函数与方程思想、化归与转化思想的考查.


全 品中考网
(17)(本小题满分10分)(注意:在试题卷上作答无效)
已知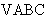 的内角
的内角 ,
,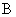 及其对边
及其对边
 ,
,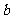
 满足
满足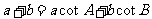 ,求内角
,求内角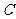 .
.
17. [命题意图]本小题主要考查三角恒等变形、利用正弦、余弦定理处理三角形中的边角关系,突出考查边角互化的转化思想的应用.
(18)(本小题满分12分)(注意:在试题卷上作答无效)
投到某杂志的稿件,先由两位初审专家进行评审.若能通过两位初审专家的评审,
则予以录用;若两位初审专家都未予通过,则不予录用;若恰能通过一位初审专家的评
审,则再由第三位专家进行复审,若能通过复审专家的评审,则予以录用,否则不予录
用.设稿件能通过各初审专家评审的概率均为0.5,复审的稿件能通过评审的概率为0.3.
各专家独立评审.
(I)求投到该杂志的1篇稿件被录用的概率;
(II)记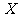 表示投到该杂志的4篇稿件中被录用的篇数,求
表示投到该杂志的4篇稿件中被录用的篇数,求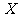 的分布列及期望.
的分布列及期望.
16.
 [命题意图]本小题主要考查椭圆的方程与几何性质、第二定义、平面向量知识,考查了数形结合思想、方程思想,本题凸显解析几何的特点:“数研究形,形助数”,利用几何性质可寻求到简化问题的捷径.
[命题意图]本小题主要考查椭圆的方程与几何性质、第二定义、平面向量知识,考查了数形结合思想、方程思想,本题凸显解析几何的特点:“数研究形,形助数”,利用几何性质可寻求到简化问题的捷径.
[解析]如图,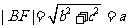 ,
,
作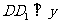 轴于点D1,则由
轴于点D1,则由 ,得
,得
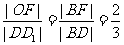 ,所以
,所以 ,
,
即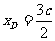 ,由椭圆的第二定义得
,由椭圆的第二定义得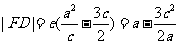
又由 ,得
,得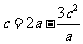 ,整理得
,整理得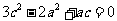 .
.
两边都除以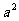 ,得
,得 ,解得
,解得
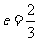 .
.
15.(1,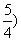 [命题意图]本小题主要考查函数的图像与性质、不等式的解法,着重考查了数形结合的数学思想.
[命题意图]本小题主要考查函数的图像与性质、不等式的解法,着重考查了数形结合的数学思想.
[解析]如图,在同一直角坐标系内画出直线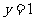 与曲线
与曲线 ,观图可知,a的取值必须满足
,观图可知,a的取值必须满足 解得
解得 .
.
(16)已知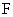 是椭圆
是椭圆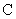 的一个焦点,
的一个焦点,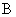 是短轴的一个端点,线段
是短轴的一个端点,线段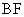 的延长线交
的延长线交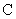 于点
于点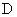 ,且
,且 ,则
,则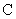 的离心率为
.
的离心率为
.
14. [命题意图]本小题主要考查三角函数值符号的判断、同角三角函数关系、和角的正切公式,同时考查了基本运算能力及等价变换的解题技能.
[命题意图]本小题主要考查三角函数值符号的判断、同角三角函数关系、和角的正切公式,同时考查了基本运算能力及等价变换的解题技能.
[解析]因为 为第三象限的角,所以
为第三象限的角,所以 ,又
,又 <0, 所以
<0, 所以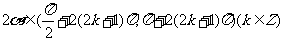 ,于是有
,于是有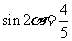 ,
,
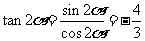 ,所以
,所以
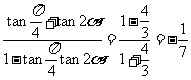 .
.
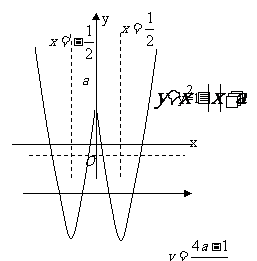 (15)直线
(15)直线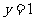 与曲线
与曲线 有四个交点,则
有四个交点,则 的取值范围是 .
的取值范围是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com