
7、在一次课外活动中,某同学对家用电器进行了相关的观察和研究,他以一台电磁炉为观察研究对象,记录了有关数据,如下表:
|
观察对象 |
有关记录和相关活动 |
|
观察电磁炉铭牌 |
U额=220V P额=1KW |
|
观察电能表的铭牌 |
220V 10(40)A 50Hz 2000r/(kw·h) |
|
用电磁炉加热一壶水 (  水的质量m=2kg,初温t=30℃) 水的质量m=2kg,初温t=30℃) |
关闭家里其它用电器,只将电磁炉接入电路烧水观察电能表,表盘在5min内转了150r,此时用温度计测得的水温为50℃。 |
请你就这位同学在活动中获得的有关资料,求解有关问题:
(1)加热时间为300S,水所吸收的热量;[已知水的比热容c=4.2×103J/(kg·℃)]
(2)电磁炉工作300S实际消耗的电能;比较(1)(2)两问的结果,说明了什么问题?
(3)电磁炉的实际功率;请你将求解结果与表中的额定功率进行比较,发现了什么问题?解释产生此问题的原因可能是什么。
6、有一质量为120g的圆柱体空玻璃瓶,按如图所示方式放置在表面积为0.1m2的水平桌面上,瓶子的底面积为0.15×10-3m2,当瓶内装满水时,瓶和水的总质量为0.45kg(g=10N/kg),求:
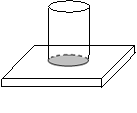 (1)玻璃瓶内水的体积为多少m3。
(1)玻璃瓶内水的体积为多少m3。
(2)装满水后玻璃瓶对水平桌面的压强。
(3)在此空瓶中装入一些金属颗粒,测得瓶和金属颗粒的总质量为0.51kg。若再在这个瓶中装满水,此时瓶、金属颗粒和水的总质量为0.79kg,求金属颗粒的密度。
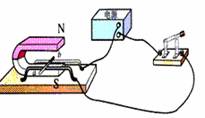
5、下图是有关电与磁实验的装置图,其中用来研究电磁铁磁性的是 。
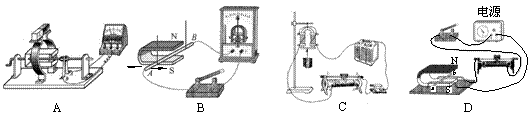
5、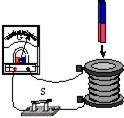 如图1,分别在冷水和热水中滴入一滴红墨水,整杯热水很快就变红了。这个现象说明: 。如图2,闭合开关后,将条形磁铁插入或拔出线圈时,电流表指针会发生偏转。这个现象说明:
。如图3,汽油机气缸内燃气膨胀推动活塞运动。这个现象说明:做功冲程
能转化为机械能。
如图1,分别在冷水和热水中滴入一滴红墨水,整杯热水很快就变红了。这个现象说明: 。如图2,闭合开关后,将条形磁铁插入或拔出线圈时,电流表指针会发生偏转。这个现象说明:
。如图3,汽油机气缸内燃气膨胀推动活塞运动。这个现象说明:做功冲程
能转化为机械能。
 |
||||||
|
|
|||||
4、如图所示是中国2010年上海世博会的核心建筑之一--中国馆,呈拱斗型。其超大的地基是通过增大受力面积,从而减小建筑主体对地面的 。中国馆的41米层观众将可乘坐轨道车进行 “智慧之旅”。游览过程中,以轨道车为参照物,游客是 的,若轨道车10min行驶了1200m,则轨道车的平均速度为 m/s。
3、、如图所示,把导线放在磁场里,在实验中发现:当接通电路,导体开始运动起来时,导体棒与金属轨道a、b接触的地方不断有火花产生,而轨道和导体不相接触处没有火花。请猜想接触处产生火花的原因可能是 ,用你学过的知识解释并支持你的猜想:

2、世博园内的“一轴四馆” 建筑已成为当今世界上首批集中应用太阳能、LED照明、冰蓄冷、地源热泵、屋面雨水收集利用、江水源循环冷却降温、气动垃圾回收、绿地节水灌溉和可再生材料使用等国际先进的“绿色”建筑技术。这里“绿色” 建筑技术从物理角度看指的是 (写一条即可)
1、电动自行车的“心脏”是电动机,它是利用 的原理工作的;关闭电源,人用力踩脚踏,电动机就变成了“发电机”,从而实现“自发电”,它的发电原理是 。
(15)(本小题共13分)
已知函数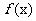
 。
。
(Ⅰ)求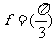 的值;
的值;
(Ⅱ)求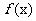 的最大值和最小值。
的最大值和最小值。
(16)(本小题共14分)
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=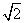 ,CE=EF=1.
,CE=EF=1.
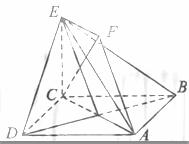
(Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:CF⊥平面BDE;
(Ⅲ)求二面角A-BE-D的大小。
(17)(本小题共13分)
某同学参加3门课程的考试。假设该同学第一门课程取得优秀成绩的概率为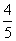 ,第二、第三门课程取得优秀成绩的概率分别为
,第二、第三门课程取得优秀成绩的概率分别为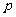 ,
,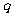 (
(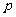 >
>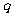 ),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
|
ξ |
0 |
1 |
2 |
3 |
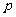 |
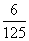 |
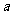 |
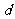 |
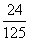 |
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求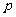 ,
,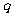 的值;
的值;
(Ⅲ)求数学期望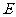 ξ。
ξ。
(18)(本小题共13分)
已知函数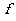 (
(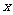 )=In(1+
)=In(1+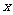 )-
)-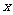 +
+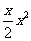 (
(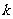 ≥0)。
≥0)。
(Ⅰ)当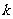 =2时,求曲线
=2时,求曲线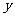 =
=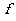 (
(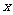 )在点(1,
)在点(1,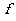 (1))处的切线方程;
(1))处的切线方程;
(Ⅱ)求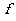 (
(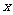 )的单调区间。
)的单调区间。
(19)(本小题共14分)
在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于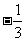 .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由。
(20)(本小题共13分)
已知集合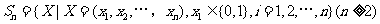 对于
对于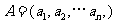 ,
,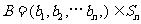 ,定义A与B的差为
,定义A与B的差为
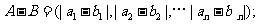
A与B之间的距离为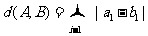
(Ⅰ)证明: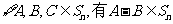 ,且
,且 ;
;
(Ⅱ)证明: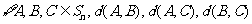 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(Ⅲ) 设P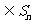 ,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为
,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为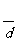 (P).
(P).
证明: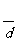 (P)≤
(P)≤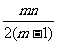 .
.
(考生务必将答案答在答题卡上,在试卷上作答无效)
()
2010年普通高等学校招生全国统一考试
(9)在复平面内,复数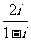 对应的点的坐标为
。
对应的点的坐标为
。
(10)在△ABC中,若b = 1,c =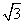 ,
,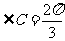 ,则a =
。
,则a =
。
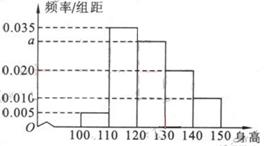 (11)从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图)。由图中数据可知a=
。若要从身高在[ 120 , 130),[130 ,140) , [140 , 150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140 ,150]内的学生中选取的人数应为
。
(11)从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图)。由图中数据可知a=
。若要从身高在[ 120 , 130),[130 ,140) , [140 , 150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140 ,150]内的学生中选取的人数应为
。
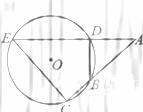
(12)如图, 的弦ED,CB的延长线交于点A。若BD
的弦ED,CB的延长线交于点A。若BD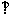 AE,AB=4, BC=2, AD=3,则DE=
;CE=
。
AE,AB=4, BC=2, AD=3,则DE=
;CE=
。
 (13)已知双曲线
(13)已知双曲线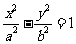 的离心率为2,焦点与椭圆
的离心率为2,焦点与椭圆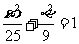 的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为
。
的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为
。
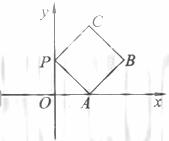
(14)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
设顶点p(x,y)的轨迹方程是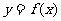 ,则
,则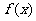 的最小正周期为
;
的最小正周期为
;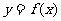 在其两个相邻零点间的图像与x轴
在其两个相邻零点间的图像与x轴
所围区域的面积为 。
说明:“正方形PABC沿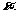 轴滚动”包括沿
轴滚动”包括沿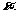 轴正方向和沿
轴正方向和沿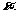 轴负方向滚动。沿
轴负方向滚动。沿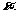 轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在
轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在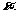 轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿
轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿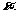 轴负方向滚动。
轴负方向滚动。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com