
1.下列四个短语,其原意一定包含化学变化的是
(A)花香四溢 (B)海市蜃楼 (C)蜡炬成灰 (D)木已成舟
22.(满分15分)已知函数f(x)=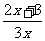 ,数列{an}满足a1=1,an+1=f(
,数列{an}满足a1=1,an+1=f(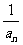 )
n
)
n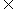 N*
N*
(1)求数列{an}的通项公式;
(2)记Tn=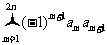 ,设数列{bn}的通项公式为bn=
,设数列{bn}的通项公式为bn= ,求bn·Tn的最大值.
,求bn·Tn的最大值.
21.(本题满分15分)已知点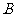 (0,1),
(0,1),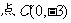 ,直线
,直线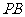 、
、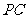 都是圆
都是圆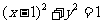 的切线(
的切线(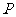 点不在
点不在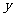 轴上). 以原点为顶点,且焦点在
轴上). 以原点为顶点,且焦点在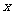 轴上的抛物线C恰好过点P.
轴上的抛物线C恰好过点P.
(1)求抛物线C的方程;
(2)过点(1,0)作直线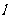 与抛物线C相交于
与抛物线C相交于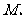
 两点,问是否存在定点
两点,问是否存在定点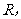 使
使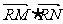 为常数?若存在,求出点
为常数?若存在,求出点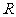 的坐标及常数;若不存在,请说明理由.
的坐标及常数;若不存在,请说明理由.
20.(本题满分14分)质地均匀的正四面体玩具的4个面上分别刻着数字1,2,3,4。将4个这样的玩具同时抛掷于桌面上。
(1)求与桌面接触的4个面上的4个数的乘积能被4整除的概率;
(2)设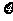 为与桌面接触的4个面上数字中偶数的个数,求
为与桌面接触的4个面上数字中偶数的个数,求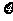 的分布列及期望E
的分布列及期望E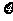 。
。
19.(本小题满分14分)
在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=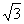 ,设D为
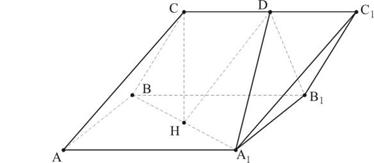
,设D为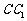 中点,
中点,
 (1)求证:
(1)求证: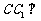 平面
平面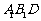 ;
;
(2)求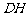 与平面
与平面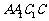 所成角的正弦值.
所成角的正弦值.
18.(本小题满分14分)
已知函数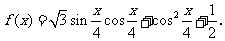
(1)求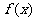 的周期和及其图象的对称中心;
的周期和及其图象的对称中心;
(2)在△ABC中,角A、B、C的对边分别是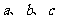 ,满足
,满足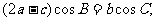 求函数
求函数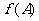 的取值范围.
的取值范围.
17.设函数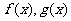 的定义域分别为
的定义域分别为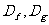 ,且
,且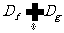 ,若
,若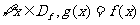 ,则函数
,则函数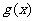 为
为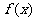 在
在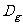 上的一个延拓函数.已知
上的一个延拓函数.已知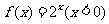 ,
,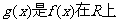 的一个延拓函数,且
的一个延拓函数,且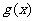 是奇函数,则
是奇函数,则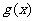 =________________
=________________
16. 如果一条直线和一个平面垂直,则称此直线与平面构成一个“正交线面对”,在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成“正交线面对”的概率为______.
15.若不等式组 表示的平面区域是一个三角形,则
表示的平面区域是一个三角形,则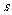 的取值范围是
.
的取值范围是
.
14.已知△AOB,点P在直线AB上,且满足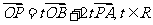 ,则
,则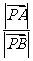 =_________
=_________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com