
20.若数列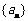 满足
满足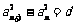 ,其中
,其中 为常数,则称数列
为常数,则称数列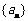 为等方差数列
为等方差数列
已知等方差数列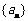 满足
满足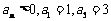 。
。
(Ⅰ)求数列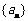 的通项公式;
的通项公式;
(Ⅱ)记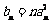 ,则当实数
,则当实数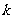 大于4时,不等式
大于4时,不等式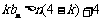 能否对于一切的
能否对于一切的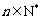 恒成立?请说明理由
恒成立?请说明理由
19.(本小题满分12分)
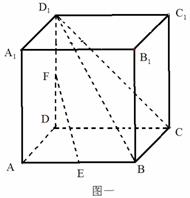
如图一所示,边长为1的正方体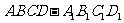 中,
中,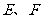 分别为
分别为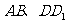 的中点。
的中点。
(Ⅰ)证明: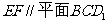 ;
;
(Ⅱ)若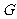 为
为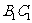 的中点,证明:
的中点,证明: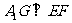 ;
;
 (Ⅲ)如图二所示为一几何体的展开图,沿着图中虚线将它们折叠起来,所得几何体的体积为
(Ⅲ)如图二所示为一几何体的展开图,沿着图中虚线将它们折叠起来,所得几何体的体积为 ,若正方体
,若正方体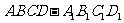 的体积为
的体积为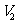 ,求
,求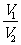 的值。
的值。
18.(本小题满分12分)
国家教育部、体育总局和共青团中央曾共同号召,在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动为此某网站于2010年1月18日至24日,在全国范围内进行了持续一周的在线调查,随机抽取其中200名大中小学生的调查情况,就每天的睡眠时间分组整理如下表所示:
序号(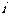 ) ) |
每天睡眠时间 (小时) |
组中值(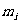 ) ) |
频数 |
频率 ( 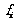 ) ) |
|
1 |
[4,5) |
4.5 |
8 |
0.04 |
|
2 |
[5,6) |
5.5 |
52 |
0.26 |
|
3 |
[6,7) |
6.5 |
60 |
0.30 |
|
4 |
[7,8) |
7.5 |
56 |
0.28 |
|
5 |
[8,9) |
8.5 |
20 |
0.10 |
|
6 |
[9,10) |
9.5 |
4 |
0.02 |
(Ⅰ)估计每天睡眠时间小于8小时的学生所占的百分比约是多少?
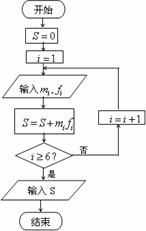
(Ⅱ)该网站利用右边的算法流程图,对样本数据作进一步统计分析,求输出的S的值,并说明S的统计意义。
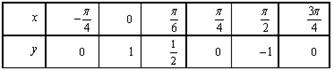
17.已知函数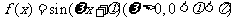 的一系列对应值如下表:
的一系列对应值如下表:
(Ⅰ)求 的解析式;
的解析式;
 (Ⅱ)若在
(Ⅱ)若在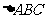 中,
中,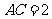 ,
,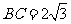 ,
,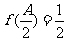 ,求∠B的值(答案也要修改)
,求∠B的值(答案也要修改)
16.某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮;现按同样的规律刺绣(小正方形的摆放规律相同),设第 个图形包含
个图形包含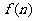 个小正方形,则
个小正方形,则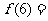 。
。

15.若直线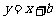 与圆
与圆 相切,则
相切,则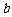 的值为
。
的值为
。
14.平面上有一组平行线,且相邻平行线间的距离为3cm,把一枚半径为1cm的硬币任意平掷在这个平面上,则硬币不与任何一条平行线相碰的概率为 。
13.已知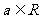 ,且
,且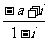 为纯虚数,则
为纯虚数,则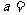 。
。
12.定义域为D的函数 同时满足条件:①常数
同时满足条件:①常数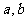 满足
满足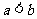 ,区间
,区间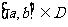 ,②使
,②使 在
在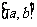 上的值域为
上的值域为 ,那么我们把
,那么我们把 叫做
叫做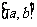 上的“
上的“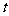 级矩形”函数.函数
级矩形”函数.函数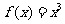 是
是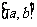 上的“1级矩形”函数,则满足条件的常数对
上的“1级矩形”函数,则满足条件的常数对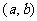 共有( )
共有( )
A.1对 B.2对 C.3对 D.4对
第Ⅱ卷(非选择题,共90分)
11.已知偶函数 在区间
在区间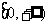 单调递增,则满足
单调递增,则满足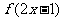 <
<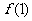 的
的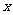 取值范围是( )
取值范围是( )
A.[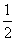 ,1)
B.(
,1)
B.(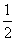 ,1) C.[0,1) D.(0,1)
,1) C.[0,1) D.(0,1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com