
21. (本小题满分12分)
设椭圆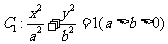 ,抛物线
,抛物线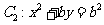 。
。
(1) 若 经过
经过 的两个焦点,求
的两个焦点,求 的离心率;
的离心率;
(2) 设A(0,b),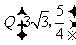 ,又M、N为
,又M、N为 与
与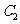 不在y轴上的两个交点,若△AMN的垂心为
不在y轴上的两个交点,若△AMN的垂心为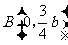 ,且△QMN的重心在
,且△QMN的重心在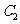 上,求椭圆
上,求椭圆 和抛物线
和抛物线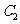 的方程。
的方程。
20. (本小题满分12分)
如图△BCD与△MCD都是边长为2的正三角形,平面MCD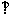 平面BCD,AB
平面BCD,AB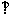 平面BCD,
平面BCD,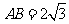 。
。
(1)
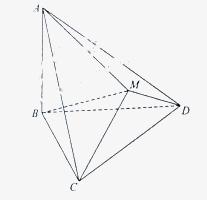 求点A到平面MBC的距离;
求点A到平面MBC的距离;
(2) 求平面ACM与平面BCD所成二面角的正弦值。
19. (本小题满分12分)
设函数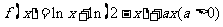 。
。
(1)当a=1时,求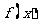 的单调区间。
的单调区间。
(2)若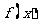 在
在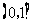 上的最大值为
上的最大值为 ,求a的值。
,求a的值。
18. (本小题满分12分)
某迷宫有三个通道,进入迷宫的每个人都要经过一扇智能门。首次到达此门,系统会随机(即等可能)为你打开一个通道,若是1号通道,则需要1小时走出迷宫;若是2号、3号通道,则分别需要2小时、3小时返回智能门。再次到达智能门时,系统会随机打开一个你未到过的通道,直至走完迷宫为止。令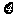 表示走出迷宫所需的时间。
表示走出迷宫所需的时间。
(1)
求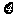 的分布列;
的分布列;
(2)
求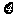 的数学期望。
的数学期望。
17.(本小题满分12分)
已知函数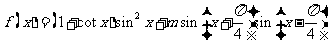 。
。
(1) 当m=0时,求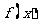 在区间
在区间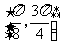 上的取值范围;
上的取值范围;
(2) 当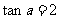 时,
时,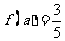 ,求m的值。
,求m的值。
16.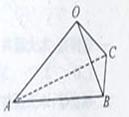 如图,在三棱锥
如图,在三棱锥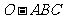 中,三条棱
中,三条棱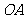 ,
, ,
,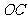 两两垂直,且
两两垂直,且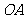 >
> >
>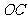 ,分别经过三条棱
,分别经过三条棱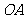 ,
, ,
,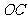 作一个截面平分三棱锥的体积,截面面积依次为
作一个截面平分三棱锥的体积,截面面积依次为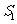 ,
, ,
,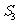 ,则
,则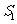 ,
, ,
,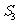 的大小关系为
。
的大小关系为
。
15.点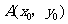 在双曲线
在双曲线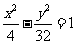 的右支上,若点A到右焦点的距离等于
的右支上,若点A到右焦点的距离等于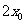 ,则
,则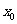 =
=
14.将6位志愿者分成4组,其中两个各2人,另两个组各1人,分赴世博会的四个不同场馆服务,不同的分配方案有 种(用数学作答)。
13.已知向量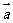 ,
,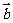 满足
满足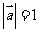 ,
,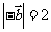 ,
, 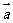 与
与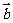 的夹角为60°,则
的夹角为60°,则
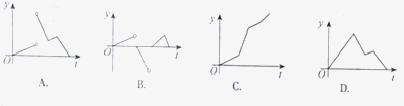
12. 如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时刻五角星露出水面部分的图形面积为
如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时刻五角星露出水面部分的图形面积为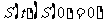 ,则导函数
,则导函数 的图像大致为
的图像大致为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com