
4.函数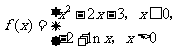 的零点个数为
的零点个数为
A.0 B.1 C.2 D.3
3.设等差数列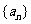 前
前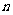 项和为
项和为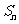 。若
。若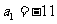 ,
,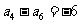 ,则
,则
当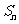 取最小值时,
取最小值时,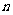 等于
等于
A.6 B.7 C.8 D.9
2.以抛物线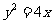 的焦点为圆心,且过坐标原点的圆的方程为
的焦点为圆心,且过坐标原点的圆的方程为
A.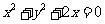 B.
B.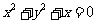
C.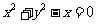 D.
D.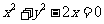
1. 计算
计算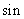 43°
43°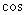 13°
13°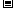
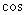 43°
43°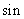 13°的结果等于
13°的结果等于
A.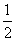 B.
B.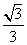 C.
C.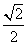 D.
D.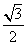
⒂(共13分)
解:(Ⅰ)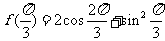 =
=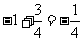
(Ⅱ)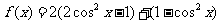
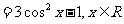
因为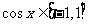 ,所以,当
,所以,当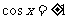 时
时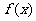 取最大值2;当
取最大值2;当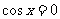 时,
时,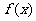 去最小值-1。
去最小值-1。
⒃(共13分)
解:(Ⅰ)设等差数列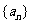 的公差
的公差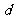 。
。
因为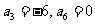
所以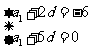 解得
解得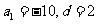
所以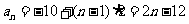
(Ⅱ)设等比数列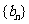 的公比为
的公比为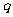
因为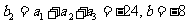
所以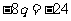 即
即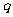 =3
=3
所以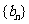 的前
的前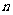 项和公式为
项和公式为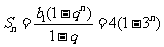
⒄(共13分)
证明:(Ⅰ)设AC于BD交于点G。因为EF∥AG,且EF=1,AG=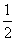 AG=1
AG=1
所以四边形AGEF为平行四边形
所以AF∥EG
因为EG 平面BDE,AF
平面BDE,AF 平面BDE,
平面BDE,
所以AF∥平面BDE
(Ⅱ)连接FG。因为EF∥CG,EF=CG=1,且CE=1,所以平行四边形CEFG为菱形。所以CF⊥EG.
因为四边形ABCD为正方形,所以BD⊥AC.又因为平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,所以BD⊥平面ACEF.所以CF⊥BD.又BD∩EG=G,所以CF⊥平面BDE.
(18)(共14分)
解:由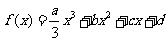 得
得 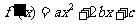
因为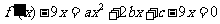 的两个根分别为1,4,所以
的两个根分别为1,4,所以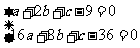 (*)
(*)
(Ⅰ)当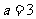 时,又由(*)式得
时,又由(*)式得
解得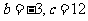
又因为曲线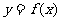 过原点,所以
过原点,所以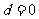
故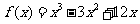
(Ⅱ)由于a>0,所以“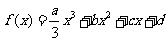 在(-∞,+∞)内无极值点”等价于“
在(-∞,+∞)内无极值点”等价于“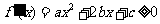 在(-∞,+∞)内恒成立”。
在(-∞,+∞)内恒成立”。
由(*)式得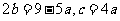 。
。
又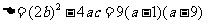
解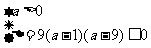 得
得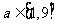
即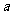 的取值范围
的取值范围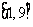
(19)(共14分)
解:(Ⅰ)因为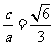 ,且
,且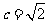 ,所以
,所以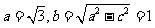
所以椭圆C的方程为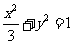
(Ⅱ)由题意知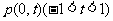
由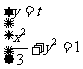 得
得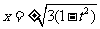
所以圆P的半径为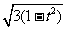
解得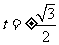 所以点P的坐标是(0,
所以点P的坐标是(0,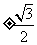 )
)
(Ⅲ)由(Ⅱ)知,圆P的方程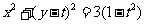 。因为点
。因为点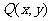 在圆P上。所以
在圆P上。所以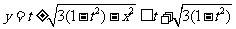
设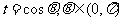 ,则
,则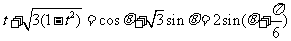
当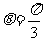 ,即
,即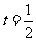 ,且
,且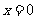 ,
,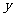 取最大值2.
取最大值2.
(20)(共13分)
(Ⅰ)解: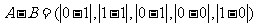 =(1,0,1,0,1)
=(1,0,1,0,1)
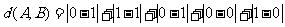 =3
=3
(Ⅱ)证明:设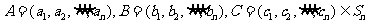
因为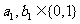 ,所以
,所以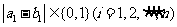
从而
由题意知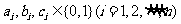
当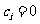 时,
时,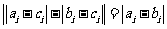
当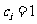 时,
时,
所以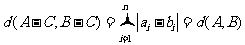
(Ⅲ)证明:设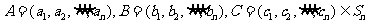
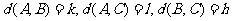
记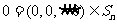 由(Ⅱ)可知
由(Ⅱ)可知
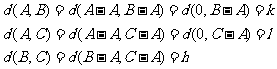
所以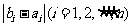 中1的个数为k,
中1的个数为k,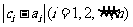 中1的个数为
中1的个数为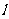
设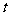 是使
是使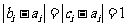 成立的
成立的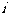 的个数。则
的个数。则
由此可知,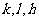 三个数不可能都是奇数
三个数不可能都是奇数
即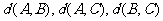 三个数中至少有一个是偶数。
三个数中至少有一个是偶数。
⑼ 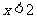
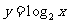 ⑽ 1
⑽ 1
⑾ -3 ⑿ 0.030 3
⒀ (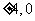 )
)
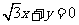 ⒁ 4
⒁ 4 
⑴ B ⑵ C ⑶ D ⑷ A
⑸ C ⑹ B ⑺ A ⑻ C
(15)(本小题共13分)
已知函数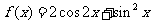
(Ⅰ)求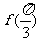 的值;
的值;
(Ⅱ)求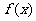 的最大值和最小值
的最大值和最小值
(16)(本小题共13分)
已知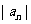 为等差数列,且
为等差数列,且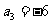 ,
,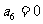 。
。
(Ⅰ)求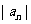 的通项公式;
的通项公式;
 (Ⅱ)若等差数列
(Ⅱ)若等差数列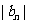 满足
满足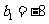 ,
,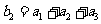 ,求
,求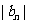 的前n项和公式
的前n项和公式
(17)(本小题共13分)
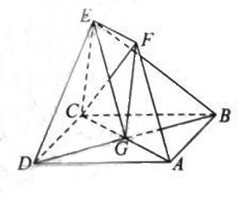
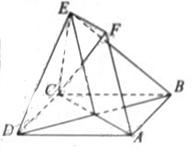
如图,正方形ABCD和四边形ACEF所在的平面互相垂直。
EF//AC,AB=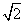 ,CE=EF=1
,CE=EF=1
(Ⅰ)求证:AF//平面BDE;
(Ⅱ)求证:CF⊥平面BDF;
(18) (本小题共14分)
设定函数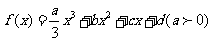 ,且方程
,且方程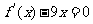 的两个根分别为1,4。
的两个根分别为1,4。
(Ⅰ)当a=3且曲线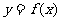 过原点时,求
过原点时,求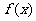 的解析式;
的解析式;
(Ⅱ)若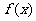 在
在 无极值点,求a的取值范围。
无极值点,求a的取值范围。
(19)(本小题共14分)
已知椭圆C的左、右焦点坐标分别是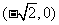 ,
,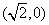 ,离心率是
,离心率是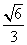 ,直线y=t椭圆C交与不同的两点M,N,以线段为直径作圆P,圆心为P。
,直线y=t椭圆C交与不同的两点M,N,以线段为直径作圆P,圆心为P。
(Ⅰ)求椭圆C的方程;
(Ⅱ)若圆P与x轴相切,求圆心P的坐标;
(Ⅲ)设Q(x,y)是圆P上的动点,当t变化时,求y的最大值。
(20)(本小题共13分)
已知集合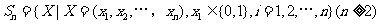 对于
对于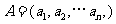 ,
,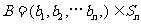 ,定义A与B的差为
,定义A与B的差为
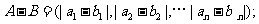
A与B之间的距离为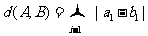
(Ⅰ)当n=5时,设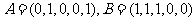 ,求
,求 ,
,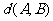 ;
;
(Ⅱ)证明: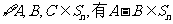 ,且
,且 ;
;
(Ⅲ) 证明: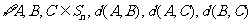 三个数中至少有一个是偶数
三个数中至少有一个是偶数
绝密«使用完毕前
2010年普通高等学校招生全国统一考试
数学(文)(北京卷)
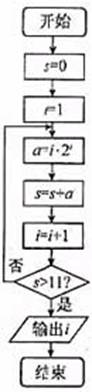
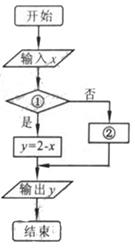
(9)已知函数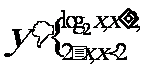 右图表示的是给
右图表示的是给
定x的值,求其对应的函数值y的程序框图,
①处应填写 ;②处应填写 。
(10)在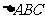 中。若
中。若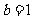 ,
,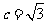 ,
,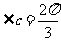 ,则a= 。
,则a= 。
 (11)若点p(m,3)到直线
(11)若点p(m,3)到直线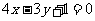 的距离为4,且点p在不等式
的距离为4,且点p在不等式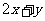 <3表示的平面区域内,则m=
。
<3表示的平面区域内,则m=
。
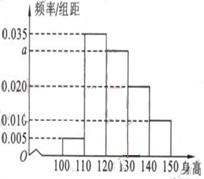
(12)从某小学随机抽取100名同学,将他们身高
(单位:厘米)数据绘制成频率分布直方图(如图)。
由图中数据可知a= 。若要从身高在
[120,130﹚,[130,140﹚,[140,150]三组内的
学生中,用分层抽样的方法选取18人参加一项活动
,则从身高在[140,150]内的学生中选取的人数
应为 。
(13)已知双曲线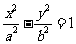 的离心率为2,焦点与椭圆
的离心率为2,焦点与椭圆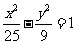 的焦点相同,那么双曲线的焦点坐标为
;渐近线方程为
。
的焦点相同,那么双曲线的焦点坐标为
;渐近线方程为
。
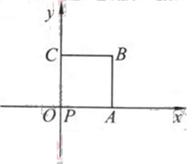
(14)如图放置的边长为1的正方形PABC沿x轴滚动。
设顶点p(x,y)的纵坐标与横坐标的函数关系是
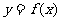 ,则
,则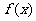 的最小正周期为
;
的最小正周期为
;
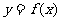 在其两个相邻零点间的图像与x轴
在其两个相邻零点间的图像与x轴
所围区域的面积为 。
说明:“正方形PABC沿x轴滚动”包含沿x轴正方向和沿x轴负方向滚动。沿x轴正方向滚动是指以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续,类似地,正方形PABC可以沿着x轴负方向滚动。
⑴ 集合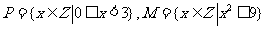 ,则
,则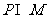 =
=
(A) {1,2} (B) {0,1,2} (C){1,2,3} (D){0,1,2,3}
⑵在复平面内,复数6+5i, -2+3i 对应的点分别为A,B.若C为线段AB的中点,则点C对应的复数是
(A)4+8i (B)8+2i (C)2+4i (D)4+i
⑶从{1,2,3,4,5}中随机选取一个数为a,从{1,2,3}中随机选取一个数为b,则b>a的概率是
(A)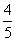 (B)
(B)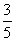 (C)
(C)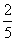 (D)
(D)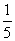
⑷若a,b是非零向量,且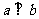 ,
,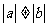 ,则函数
,则函数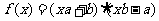 是
是
(A)一次函数且是奇函数 (B)一次函数但不是奇函数
(C)二次函数且是偶函数 (D)二次函数但不是偶函数
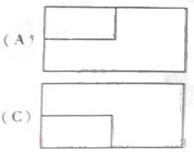
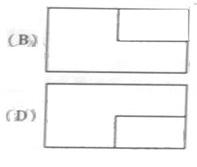
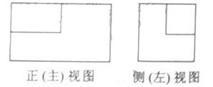 (5)一个长方体去掉一个小长方体,所得几何体的
(5)一个长方体去掉一个小长方体,所得几何体的
正(主)视图与侧(左)视图分别如右图所示,则该
集合体的俯视图为:
(6)给定函数①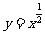 ,②
,②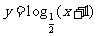 ,③
,③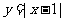 ,④
,④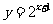 ,期中在区间(0,1)上单调递减的函数序号是
,期中在区间(0,1)上单调递减的函数序号是
(A)①② (B)②③ (C)③④ (D)①④
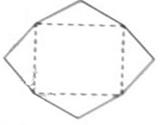 (7)某班设计了一个八边形的班徽(如图),它由腰长为1,
(7)某班设计了一个八边形的班徽(如图),它由腰长为1,
顶角为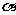 的四个等腰三角形,及其底边构成的正方形所组成,
的四个等腰三角形,及其底边构成的正方形所组成,
该八边形的面积为
(A)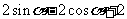 ;
(B)
;
(B)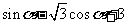
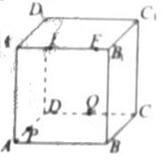 (C)
(C)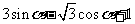 ; (D)
; (D)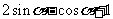
(8)如图,正方体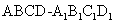 的棱长为2,
的棱长为2,
动点E、F在棱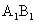 上。点Q是CD的中点,动点
上。点Q是CD的中点,动点
P在棱AD上,若EF=1,DP=x,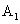 E=y(x,y大于零),
E=y(x,y大于零),
则三棱锥P-EFQ的体积:
(A)与x,y都有关; (B)与x,y都无关;
 (C)与x有关,与y无关; (D)与y有关,与x无关;
(C)与x有关,与y无关; (D)与y有关,与x无关;
第Ⅱ卷(共110分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com