6.从空中某一位置以大小为v₀的速度水平抛出一质量为m的物体，经过时间t，物体下落一段距离h后，其速度大小仍为v₀，但方向与初速度方向相反，如图所示.下列说法错误的是(　)

A.风力对物体做功为零

B.风力对物体做负功，其大小等于物体机械能的变化

C.物体机械能减少mgh

D.物体机械能减少mg²t²

解析：物体在空中运动的过程中，重力和风力对其做功，由动能定理得：

W_风+mgh＝0

可得：W_风＝－mgh

由题意知，物体机械能的变化ΔE＝－mgh

若物体在竖直方向的受力恒为mg，则有：

h＝gt²

又由前面所述知风力对物体做负功，即风力方向为斜向上，则物体竖直方向的加速度a＜g，可得h＜gt²，|ΔE_p|＜mg²t².

答案：AD

5.如图所示，某人用竖直向上的力缓慢提起长为L、质量为m的置于地面上的铁链，则在将铁链提起到刚要脱离地面的过程中，提力所做的功为(　)

A.mgL　B.mgL　C.mgL　D.mgL

解析：缓慢提起的过程中铁链动能不变，由功能原理得：

W_F＝ΔE_机＝mgL.

答案：B

4.如图所示，卷扬机的绳索通过定滑轮用力F拉位于粗糙斜面上的木箱，使之沿斜面加速向上移动.在移动过程中，下列说法正确的是(　)

A.F对木箱做的功等于木箱增加的动能与木箱克服摩擦力所做的功之和

B.F对木箱做的功等于木箱克服摩擦力和克服重力所做的功之和

C.木箱克服重力所做的功等于木箱增加的重力势能

D.F对木箱做的功等于木箱增加的机械能与木箱克服摩擦力做的功之和

解析：设木箱克服重力做的功为W_G，克服摩擦力做的功为W_f.

由动能定理有：W_F－W_f－W_G＝ΔE_k

即：W_F＝ΔE_k+W_G+W_f＝ΔE_k+ΔE_p+W_f

故选项D正确.

克服重力做的功W_G＝ΔE_p，故选项C正确.

答案：CD

3.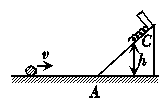如图所示，固定在地面上的光滑斜面的顶端固定有一弹簧，一物体在光滑的水平地面上向右滑行并冲上斜面.已知物体在斜面最低点A时的速度为v，压缩弹簧至C点时弹簧最短，C点距地面的高度为h，则从A到C的过程中，弹簧弹力做的功是(　)

A.mgh－mv²　　　B.mv²－mgh

C.－mgh　 D.－(mgh+mv²)

解析：令弹簧弹力做的功为W，在A→C的过程中由动能定理得：

W－mgh＝0－mv²

所以W＝mgh－mv²，故选项A正确.

答案：A

2.从地面竖直上抛一个质量为m的小球，小球上升的最大高度为H.设上升过程中空气阻力F_阻恒定，对于小球的整个上升过程，下列说法错误的是(　)

A.小球动能减少了mgH

B.小球机械能减少了F_阻H

C.小球重力势能增加了mgH

D.小球的加速度大于重力加速度g

解析：动能的变化ΔE_k＝－mgH－F_阻H，选项A错误；机械能的变化ΔE＝－F_阻H，选项B正确；小球重力势能的变化ΔE_p＝mgH，选项C正确；由牛顿第二定律得a＝＞g，选项D正确.

答案：A

1.行驶中的汽车制动后滑行一段距离，最后停下；流星在夜空中坠落并发出明亮的光焰；降落伞在空中匀速下降；条形磁铁在下落过程中穿过闭合线圈，线圈中产生电流.上述不同现象中所包含的相同物理过程是(　)

A.重力对物体做功

B.物体的动能转化为其他形式的能量

C.物体的势能转化为其他形式的能量

D.物体的机械能转化为其他形式的能量

解析：汽车在水平路面上的制动过程，重力对其不做功，选项A、C错误；降落伞匀速下降时动能并没有变化，选项B错误.上述各物理过程中减少的机械能转化成其他形式的能量，选项D正确.

答案：D

6.如图甲所示，物块A的质量m＝2 kg；木板B长L＝1 m，质量M＝3 kg.开始时两物体静止，且A在B最右端，现用F＝24 N的水平拉力拉着轻质滑轮水平向左运动，经过一段时间，物块A滑到木板最左端，不计一切摩擦，求：

(1)此时物块A的速度.

(2)这个过程中拉力F做的功.

解析：(1)如图乙所示，用F＝24 N的力拉动滑轮时，A、B受到向左的拉力均为F′＝12 N

由牛顿第二定律知：a_A＝＝6 m/s²

a_B＝＝4 m/s²

当A滑到木板左端时，有：

a_At²－a_Bt²＝L

解得：t＝1 s

此时v_A＝a_At＝6 m/s

v_B＝a_Bt＝4 m/s.

(2)解法一　由功能关系知，拉力F做的功等于A、B机械能的增量.

W_F＝mv+Mv＝60 J.

解法二　A滑到B左端时，B的位移为：

s_B＝a_Bt²＝2 m

故动滑轮的位移s＝s_B+＝2.5 m

拉力做的功W_F＝F·s＝60 J.

答案：(1)4 m/s　(2)60 J

金典练习十三　功能关系　能的转化与守恒定律

选择题部分共10小题，每小题6分.在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确.

5.如图甲所示，在高为1.5 m的光滑平台上有一个质量为2 kg的小球被一细线拴在墙上，球与墙之间有一根被压缩的轻质弹簧.当细线被烧断时，小球被弹出，小球落地时的速度方向与水平方向成60°角.求弹簧被压缩时具有的弹性势能.(取g＝10 m/s²)

解析：设小球落地前瞬间的速度为v，将v沿水平和竖直方向正交分解，如图乙所示，有：

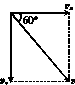v_y＝＝ m/s

v＝＝2 m/s

对于细线被烧断后的过程，由动能定理，有：

mgh+W_弹＝mv²－0

解得：W_弹＝10 J

弹簧被压缩时具有的弹性势能等于细线被烧断后弹簧对小球做的功，即E_p＝W_弹＝10 J.

答案：10 J

4.在盛水的一个杯子里有一木块，开始时木块被一根细绳拴住而完全没入水中，如图所示，整个装置与外界绝热，断开细绳，则木块将浮在水面上，最后达到平衡，在这一过程中，水、杯子和木块组成的系统(　)

A.内能增大　　　B.内能减小

C.内能不变　 D.条件不足，无法判断

解析：断开细绳后木块上升至水面，木块原来所处的位置被水填充，故水与木块组成的系统重心下降、重力势能减小.由能的转化和守恒定律知，系统的内能增大.

答案：A

3.如图所示，M、N是固定的半圆形轨道的两个端点，轨道半径为R，一个质量为m的小球从M点正上方高为H处自由落下，正好沿切线进入轨道，M、N两点等高，小球离开N点后能上升的最大高度为.不计空气阻力，小球在此过程中克服半圆轨道摩擦力做的功为W；小球到最高点后又落回半圆轨道，向左侧滑动.则下列说法正确的是(　)

A.W＝mgH，小球恰好能向左滑至M点

B.W＝mgH，小球能向左滑出M点并继续上升一定高度

C.W＜mgH，小球恰好能向左滑至M点

D.W＜mgH，小球能向左滑出M点并继续上升一定高度

解析：小球从H高处下落经轨道后又上升至H高处的过程，由动能定理有：

mg(H－)－W＝0

得：W＝mgH

设小球再次落下后向左滑至M点时的速度为v_M，由动能定理：mg－W′＝mv

又因为向左滑过半圆轨道时经过每一点的速率都小于向右滑过时的速率，故小球对半圆轨道的压力以及半圆轨道对小球的摩擦力都小于前次向右滑过轨道该处的数值，可得W′＜W，v_M＞0，即小球能滑出M点后又继续上升一定高度.

答案：B