
19.(本小题满分12分,(Ⅰ)小问6分,(Ⅱ)小问6分)
直四棱柱 中,底面
中,底面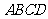 为菱形,且
为菱形,且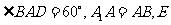 为
为
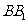 延长线上的一点,
延长线上的一点, 面
面 .
.
(Ⅰ)求二面角 的大小;(Ⅱ)在
的大小;(Ⅱ)在 上是否存在一点
上是否存在一点 ,使
,使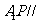 面
面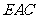 .
.
 若存在,求
若存在,求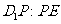 的值;不存在,说明理由.
的值;不存在,说明理由.
[解]:(Ⅰ)连接 交
交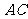 于点
于点 ,连接
,连接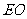
、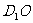 ;∵
;∵ ,∴
,∴ ≌
≌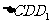 ,
,
 ,同理可证
,同理可证
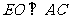 ,∴
,∴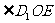 就是二面角
就是二面角
的平面角。设 ,
, ,
,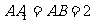
∵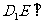 平面
平面 ;∴
;∴ ,∴在
,∴在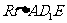
中 ;
;
又连接 ,在
,在 中,
中,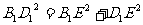 ,∴
,∴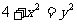 ,联立方程组解得
,联立方程组解得
 ,∴
,∴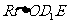 中,记
中,记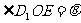 ,∴
,∴ .
.
(Ⅱ)存在这样的点 ,当
,当 时,
时,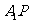 ∥平面
∥平面 .证明如下:
.证明如下:
连接 ,
, 相交于点
相交于点 ,过点
,过点 作
作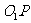 ∥
∥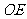 交
交 于
于 ,连接
,连接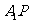 .
.
由于 ∥
∥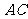 ,
,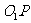 ∥
∥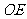 ,∴平面
,∴平面 ∥平面
∥平面 ;∴
;∴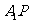 ∥平面
∥平面 。
。
设 ,则
,则 ,∴
,∴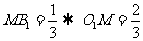 ,所以
,所以 .
.
18.(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分)
若函数 在点
在点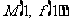 处的切线方程为
处的切线方程为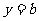
(Ⅰ)求 的值及
的值及 的单调递减区间;
的单调递减区间;
(Ⅱ)若对于任意的 ,恒有
,恒有 成立,求实数
成立,求实数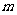 的取值范围(其中
的取值范围(其中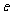 为自然对数的底数).
为自然对数的底数).
[解]:(Ⅰ)因为 ,由题意得
,由题意得
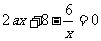 ,得
,得
则 ,由题意
,由题意
故 ,
, ……………………………………(3分)
……………………………………(3分)
令 ,则
,则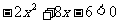
 ,
, 或
或
即 的单调递增区间为
的单调递增区间为
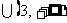 ………………………(6分)
………………………(6分)
(Ⅱ)因为 ,又由(Ⅰ)知函数
,又由(Ⅰ)知函数 在区间
在区间 上为增函数,在
上为增函数,在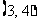 上为减函数,
上为减函数,
所以 ;
;
又 ,由题意
,由题意 ,解之得
,解之得
故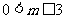 …………(12分)
…………(12分)
17.(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分)
盒中装有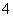 个大小形状相同的小球,球上分别标有号码
个大小形状相同的小球,球上分别标有号码 ,
, ,
, ,
, ,从盒中有放回地抽取两个小球(每次抽取一个小球).
,从盒中有放回地抽取两个小球(每次抽取一个小球).
(Ⅰ)求这两个小球号码不相同的概率;
(Ⅱ)记 为这两个小球上号码的乘积,求随机变量
为这两个小球上号码的乘积,求随机变量 的分布列及其数学期望
的分布列及其数学期望 ;
;
[解]:(Ⅰ)两小球都为0或都为2的概率均为: ,都为1的概率为:
,都为1的概率为:
∴ 所求概率 ·········································································· 6分
·········································································· 6分
(Ⅱ)

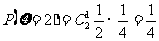
 ·························· 10分
·························· 10分
∴ 的分布列为
的分布列为
 |
0 |
1 |
2 |
4 |
|
P |
 |
 |
 |
 |
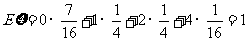 ………………13分
………………13分
16.(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分)
已知 中角A、B、C的对边分别为
中角A、B、C的对边分别为
(Ⅰ)求 的值;(Ⅱ)求
的值;(Ⅱ)求 的值。
的值。
[解]:(Ⅰ)在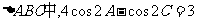
 (2分)
(2分)
 (4分)
(4分)
根据正弦定理:
于是 (6分)
(6分)
(Ⅱ)在 中,根据余弦定理,得
中,根据余弦定理,得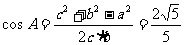
于是
从而
 (12分)
(12分)
所以 (13分)
(13分)
15.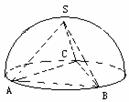 如图,已知各顶点都在半球面上的正三棱锥,其侧面积为
如图,已知各顶点都在半球面上的正三棱锥,其侧面积为 ,
,
则这个球的表面积是 .
.
14.设 为双曲线
为双曲线 的左焦点,在
的左焦点,在 轴上
轴上 点的右侧有一点
点的右侧有一点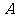 ,以
,以 为直径的圆与双
为直径的圆与双
曲线左、右两支在 轴上方的交点分别为
轴上方的交点分别为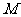 、
、 ,则
,则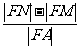 的值为
的值为 ;
;
13.已知函数 在R上连续,则
在R上连续,则
 .
.
12.已知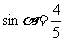 ,
, ,
, ,则
,则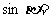
 .
.
11.已知向量 ,向量
,向量 ,且
,且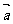 ∥
∥ ,则
,则 的值是
的值是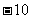 .
.
10.已知 ,若对任意两个不等的正实数
,若对任意两个不等的正实数 都有
都有
 恒成立,则
恒成立,则 的取值范围是( B )
的取值范围是( B )
A. B.
B. C.
C. D.
D.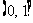
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com