
3. 右图是2010年上海世博会会徽图案,请仔细观察,写一段解说文字。要求解说内容包含构成要素、造型特点、含义等;语言简练,至少用上一个成语。(3分)
右图是2010年上海世博会会徽图案,请仔细观察,写一段解说文字。要求解说内容包含构成要素、造型特点、含义等;语言简练,至少用上一个成语。(3分)
2.改正下列句子中的语病。(2分)
①通过参加这次为玉树灾区捐款捐物活动,让我领会了“同舟共济”的精神内涵。
②我们既要有效化解各种矛盾,又要积极营造良好环境,不断促进社会和谐是社会发展的
必然要求。
1.根据拼音写出汉字,给加点的字注音。(2分)
微笑是一缕轻柔的春雨,可以平息肆nüè的狂风;微笑是一颗闪亮的星辰,可以慰藉夜间跋涉者的心灵;微笑也是一座坚实的精神桥墩,可以承载千万吨的重负。
①nüè ②载
(17)(本小题满分10分)(注意:在试题卷上作答无效)
记等差数列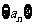 的前
的前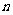 项和为
项和为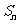 ,设
,设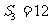 ,且
,且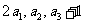 成等比数列,求
成等比数列,求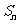 .
.

(18)(本小题满分12分)(注意:在试题卷上作答无效)
已知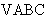 的内角
的内角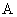 ,
,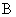 及其对边
及其对边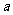 ,
,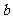 满足
满足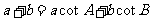 ,求内角
,求内角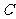 .
.
(18)、解:
由
 及正弦定理得
及正弦定理得
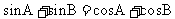 ,
,
 ,
,
从而 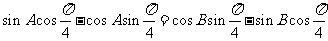 ,
,
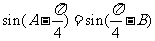 .
.
又
故 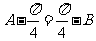
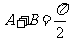 ,
,
所以 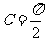 .
.
(19)(本小题满分12分)(注意:在试题卷上作答无效)
投到某杂志的稿件,先由两位初审专家进行评审.若能通过两位初审专家的评审,
则予以录用;若两位初审专家都未予通过,则不予录用;若恰能通过一位初审专家的评
审,则再由第三位专家进行复审,若能通过复审专家的评审,则予以录用,否则不予录
用.设稿件能通过各初审专家评审的概率均为0.5,复审的稿件能通过评审的概率为0.3.
各专家独立评审.
(I)求投到该杂志的1篇稿件被录用的概率;
(II)求投到该杂志的4篇稿件中,至少有2篇被录用的概率.
(19)、解:
(Ⅰ)记 A表示事件:稿件能通过两位初审专家的评审;
B表示事件:稿件恰能通过一位初审专家的评审;
C表示事件:稿件能通过复审专家的评审;
D表示事件:稿件被录用.
则 D=A+B·C,
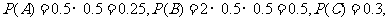
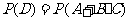
=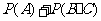

 =
=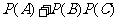
=0.25+0.5×0.3
=0.40.

(20)(本小题满分12分)(注意:在试题卷上作答无效)
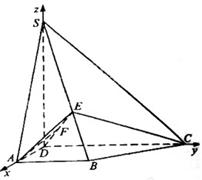
如图,四棱锥S-ABCD中,SD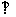 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD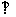 DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC
DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC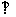 平面SBC .
平面SBC .
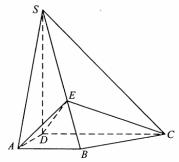
(Ⅰ)证明:SE=2EB;
(Ⅱ)求二面角A-DE-C的大小 .
(20)解法一:
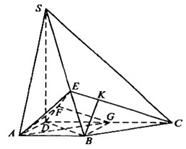 (Ⅰ)连接BD,取DC的中点G,连接BG,
(Ⅰ)连接BD,取DC的中点G,连接BG,
由此知 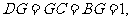 即
即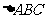 为直角三角形,故
为直角三角形,故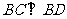 .
.
又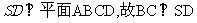 ,
,
所以,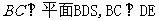 .
.
作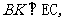
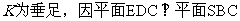 ,
,
故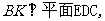
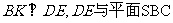 内的两条相交直线
内的两条相交直线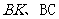 都垂直.
都垂直.
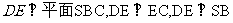

 ,
,
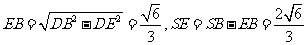 ,
,
所以,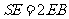 .
.

解法二:
以D为坐标原点,射线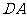 为
为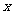 轴的正半轴,建立如图所示的直角坐标系
轴的正半轴,建立如图所示的直角坐标系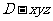 ,
,
设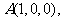 则
则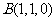 ,
,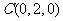 ,
,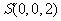 .
.
(Ⅰ)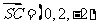 ,
, 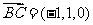
 设平面
设平面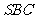 的法向量为
的法向量为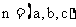 ,
,
由 ,
,

(Ⅱ) 由(Ⅰ)知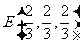 ,取
,取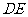 中点F,则
中点F,则
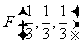 ,
,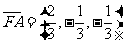 ,
,
故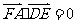 ,由此得
,由此得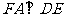 .
.
又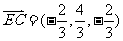 ,故
,故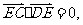 由此得
由此得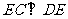 ,
,
向量 与
与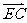 的夹角等于二面角
的夹角等于二面角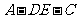 的平
的平 面角.
面角.
于是
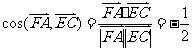 ,
,
所以,二面角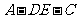 的大小为120°.
的大小为120°.
(21)(本小题满分12分)(注意:在试题卷上作答无效)
已知函数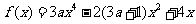
(I)当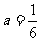 时,求
时,求 的极值;
的极值;
(II)若 在
在 上是增函数,求
上是增函数,求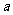 的取值范围
的取值范围
(21)、解:(Ⅰ)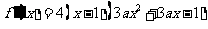
当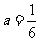 时,
时,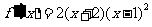 ,
, 在
在 内单调减,在
内单调减,在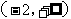 内单调增,在
内单调增,在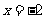 时,
时, 有极小值.
有极小值.
所以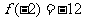 是
是 的极小值.
的极小值.

(22)(本小题满分12分)(注意:在试题卷上作答无效)
已知抛物线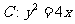 的焦点为F,过点
的焦点为F,过点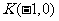 的直线
的直线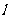 与
与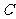 相交于
相交于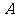 、
、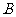 两点,点A关于
两点,点A关于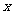 轴的对称点为D .
轴的对称点为D .
(Ⅰ)证明:点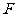 在直线
在直线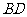 上;
上;
(Ⅱ)设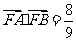 ,求
,求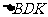 的内切圆
的内切圆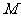 的方程 .
的方程 .
(22)、解:
设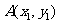 ,
, ,
,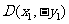 ,
,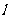 的方程为
的方程为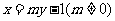 .
.
(Ⅰ)将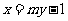 代人
代人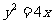 并整理得
并整理得
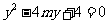 ,
,
从而 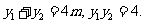
直线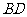 的方程为
的方程为
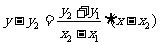 ,
,
即 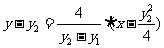
令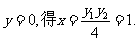
所以点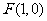 在直线
在直线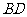 上
上
(Ⅱ)由①知,
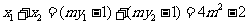
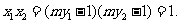
因为 
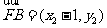 ,
,
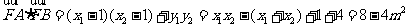
故 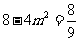 ,
,
解得 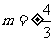
所以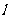 的方程为
的方程为

又由①知 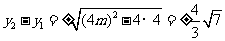
故直线BD的斜率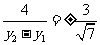 ,
,
因而直线BD的方程为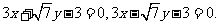

16. 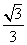 [命题意图]本小题主要考查椭圆的方程与几何性质、第二定义、平面向量知识,考查了数形结合思想、方程思想,本题凸显解析几何的特点:“数研究形,形助数”,利用几何性质可寻求到简化问题的捷径.
[命题意图]本小题主要考查椭圆的方程与几何性质、第二定义、平面向量知识,考查了数形结合思想、方程思想,本题凸显解析几何的特点:“数研究形,形助数”,利用几何性质可寻求到简化问题的捷径.
 [解析1]如图,
[解析1]如图,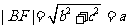 ,
,
作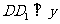 轴于点D1,则由
轴于点D1,则由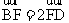 ,得
,得
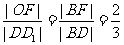 ,所以
,所以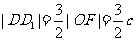 ,
,
即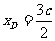 ,由椭圆的第二定义得
,由椭圆的第二定义得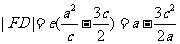
又由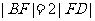 ,得
,得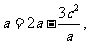
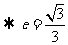
[解析2]设椭圆方程为第一标准形式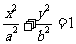 ,设
,设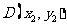 ,F分 BD所成的比为2,
,F分 BD所成的比为2,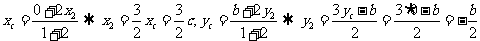 ,代入
,代入
 ,
,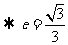
15. A[命题意图]本小题主要考查分类计数原理、组合知识,以及分类讨论的数学思想.
[解析1]:可分以下2种情况:(1)A类选修课选1门,B类选修课选2门,有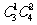 种不同的选法;(2)A类选修课选2门,B类选修课选1门,有
种不同的选法;(2)A类选修课选2门,B类选修课选1门,有 种不同的选法.所以不同的选法共有
种不同的选法.所以不同的选法共有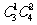 +
+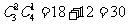 种.
种.
[解析2]: 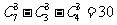
(16)已知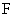 是椭圆
是椭圆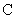 的一个焦点,
的一个焦点,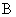 是短轴的一个端点,线段
是短轴的一个端点,线段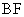 的延长线交
的延长线交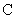 于点
于点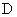 , 且
, 且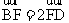 ,则
,则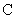 的离心率为
.
的离心率为
.
(注意:在试题卷上作答无效)
(13)不等式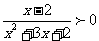 的解集是 .
的解集是 .
13.
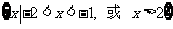 [命题意图]本小题主要考查不等式及其解法
[命题意图]本小题主要考查不等式及其解法
[解析]: 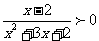
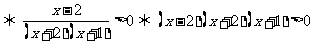 ,数轴标根得:
,数轴标根得: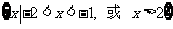
(14)已知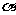 为第二象限的角,
为第二象限的角, ,则
,则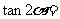 .
.
14.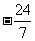 [命题意图]本小题主要考查三角函数值符号的判断、同角三角函数关系、和角的正切公式,同时考查了基本运算能力及等价变换的解题技能.
[命题意图]本小题主要考查三角函数值符号的判断、同角三角函数关系、和角的正切公式,同时考查了基本运算能力及等价变换的解题技能.
[解析]因为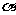 为第二象限的角,又
为第二象限的角,又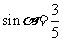 , 所以
, 所以 ,
,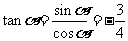 ,所
,所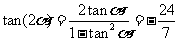
(15)某学校开设A类选修课3门,B类选修课4门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有 种.(用数字作答)
3.第Ⅱ卷共10小题,共90分。
2.第Ⅱ卷共2页,请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域
内作答,在试题卷上作答无效。
12.B[命题意图]本小题主要考查几何体的体积的计算、球的性质、异面直线的距离,通过球这个载体考查考生的空间想象能力及推理运算能力.
[解析]过CD作平面PCD,使AB⊥平面PCD,交AB与P,设点P到CD的距离为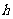 ,则有
,则有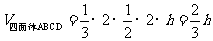 ,当直径通过AB与CD的中点时,
,当直径通过AB与CD的中点时,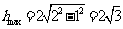 ,故
,故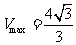 .
.
第Ⅱ卷
证号填写清楚,然后贴好条形码。请认真核准条形码上的准考证号、姓名和科目。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com