
11.D[命题意图]本小题主要考查向量的数量积运算与圆的切线长定理,着重考查最值的求法——判别式法,同时也考查了考生综合运用数学知识解题的能力及运算能力.
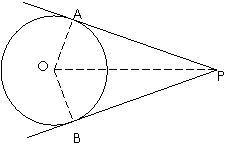 [解析1]如图所示:设PA=PB=
[解析1]如图所示:设PA=PB=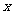
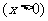 ,∠APO=
,∠APO=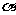 ,则∠APB=
,则∠APB=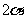 ,PO=
,PO=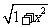 ,
,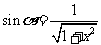 ,
,
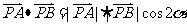 =
=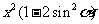 =
=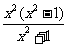 =
=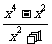 ,令
,令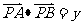 ,则
,则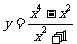 ,即
,即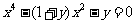 ,由
,由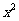 是实数,所以
是实数,所以
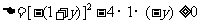 ,
,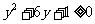 ,解得
,解得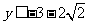 或
或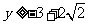 .故
.故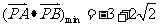 .此时
.此时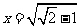 .
.
[解析2]设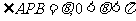 ,
,
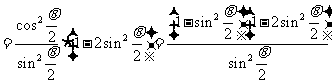 换元:
换元: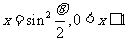 ,
,
[解析3]建系:园的方程为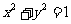 ,设
,设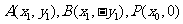 ,
,
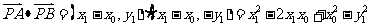
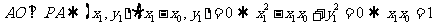
(12)已知在半径为2的球面上有A、B、C、D四点,若AB=CD=2,则四面体ABCD的体积的最大值为
(A) 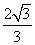 (B)
(B)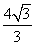 (C)
(C) 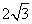 (D)
(D) 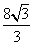
10.C [命题意图]本小题以指数、对数为载体,主要考查指数函数与对数函数的性质、实数大小的比较、换底公式、不等式中的倒数法则的应用.
[解析1] a=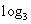 2=
2=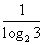 , b=In2=
, b=In2=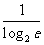 ,而
,而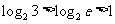 ,所以a<b,
,所以a<b,
c= =
=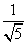 ,而
,而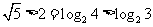 ,所以c<a,综上c<a<b.
,所以c<a,综上c<a<b.
[解析2]a=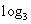 2=
2=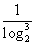 ,b=ln2=
,b=ln2=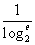 ,
, 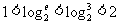 ,
,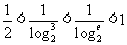 ; c=
; c=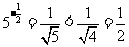 ,∴c<a<b
,∴c<a<b
(11)已知圆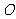 的半径为1,PA、PB为该圆的两条切线,A、B为两切点,那么
的半径为1,PA、PB为该圆的两条切线,A、B为两切点,那么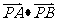 的最小值为
的最小值为
(A)  (B)
(B) (C)
(C)  (D)
(D)
9.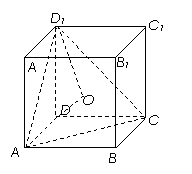 D [命题意图]本小题主要考查正方体的性质、直线与平面所成的角、点到平面的距离的求法,利用等体积转化求出D到平面AC
D [命题意图]本小题主要考查正方体的性质、直线与平面所成的角、点到平面的距离的求法,利用等体积转化求出D到平面AC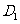 的距离是解决本题的关键所在,这也是转化思想的具体体现.
的距离是解决本题的关键所在,这也是转化思想的具体体现.
[解析1]因为BB1//DD1,所以B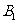 与平面AC
与平面AC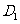 所成角和DD1与平面AC
所成角和DD1与平面AC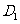 所成角相等,设DO⊥平面AC
所成角相等,设DO⊥平面AC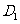 ,由等体积法得
,由等体积法得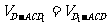 ,即
,即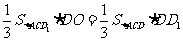 .设DD1=a,
.设DD1=a,
则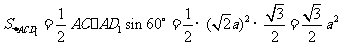 ,
,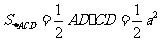 .
.
所以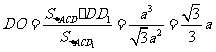 ,记DD1与平面AC
,记DD1与平面AC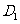 所成角为
所成角为 ,则
,则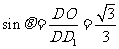 ,所以
,所以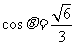 .
.
[解析2]设上下底面的中心分别为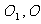 ;
;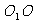 与平面AC
与平面AC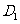 所成角就是B
所成角就是B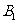 与平面AC
与平面AC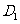 所成角,
所成角,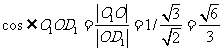
(10)设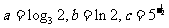 则
则
(A) (B)
(B)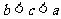 (C)
(C) 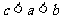 (D)
(D) 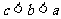
8.B[命题意图]本小题主要考查双曲线定义、几何性质、余弦定理,考查转化的数学思想,通过本题可以有效地考查考生的综合运用能力及运算能力.
[解析1].由余弦定理得
cos∠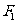 P
P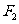 =
=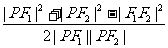
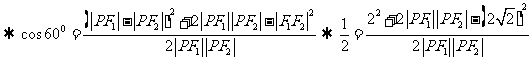
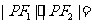 4
4
[解析2]由焦点三角形面积公式得: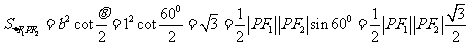
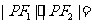 4
4
(9)正方体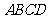 -
-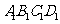 中,
中, 与平面
与平面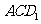 所成角的余弦值为
所成角的余弦值为
(A) 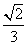 (B)
(B)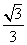 (C)
(C)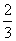 (D)
(D)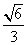
7.C[命题意图]本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a的取值范围,而利用均值不等式求得a+b=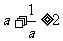 ,从而错选D,这也是命题者的用苦良心之处.
,从而错选D,这也是命题者的用苦良心之处.
[解析1]因为 f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去),或 ,所以a+b=
,所以a+b=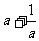
又0<a<b,所以0<a<1<b,令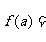
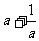 由“对勾”函数的性质知函数
由“对勾”函数的性质知函数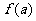 在
在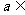 (0,1)上为减函数,所以f(a)>f(1)=1+1=2,即a+b的取值范围是(2,+∞).
(0,1)上为减函数,所以f(a)>f(1)=1+1=2,即a+b的取值范围是(2,+∞).
[解析2]由0<a<b,且f(a)=f(b)得: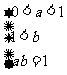 ,利用线性规划得:
,利用线性规划得: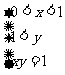 ,化为求
,化为求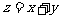 的取值范围问题,
的取值范围问题,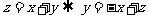 ,
,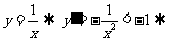 过点
过点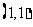 时z最小为2,∴(C)
时z最小为2,∴(C) 
(8)已知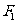 、
、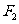 为双曲线C:
为双曲线C: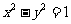 的左、右焦点,点P在C上,∠
的左、右焦点,点P在C上,∠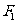
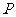
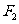 =
=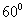 ,则
,则
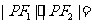
(A)2 (B)4 (C) 6 (D) 8
6.C[命题意图]本小题主要考查直三棱柱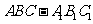 的性质、异面直线所成的角、异面直线所成的角的求法.
的性质、异面直线所成的角、异面直线所成的角的求法.
[解析]延长CA到D,使得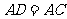 ,则
,则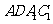 为平行四边形,
为平行四边形,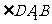 就是异面直线
就是异面直线
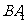 与
与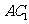 所成的角,又三角形
所成的角,又三角形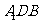 为等边三角形,
为等边三角形,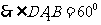
(7)已知函数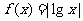 .若
.若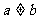 且,
且,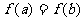 ,则
,则 的取值范围是
的取值范围是
(A) (B)
(B) (C)
(C)  (D)
(D) 
5.A. [命题意图]本小题主要考查了考生对二项式定理的掌握情况,尤其是展开式的通项公式的灵活应用,以及能否区分展开式中项的系数与其二项式系数,同时也考查了考生的一些基本运算能力.
[解析]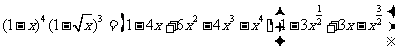
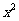 的系数是 -12+6=-6
的系数是 -12+6=-6
(6)直三棱柱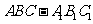 中,若
中,若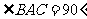 ,
,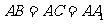 ,则异面直线
,则异面直线
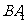 与
与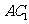 所成的角等于
所成的角等于
(A)30° (B)45°(C)60° (D)90°
4.A[命题意图]本小题主要考查等比数列的性质、指数幂的运算、根式与指数式的互化等知识,着重考查了转化与化归的数学思想.
[解析]由等比数列的性质知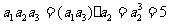 ,
,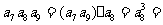 10,所以
10,所以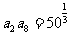 ,
,
所以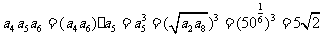
(5)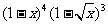 的展开式
的展开式 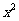 的系数是
的系数是
(A)-6 (B)-3 (C)0 (D)3
3.B [命题意图]本小题主要考查线性规划知识、作图、识图能力及计算能力.
[解析]画出可行域(如右图),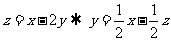 ,由图可知,当直线
,由图可知,当直线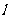 经过点A(1,-1)时,z最大,且最大值为
经过点A(1,-1)时,z最大,且最大值为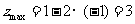 .
.

(4)已知各项均为正数的等比数列{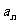 },
},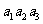 =5,
=5,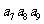 =10,则
=10,则
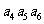 =
=
(A) 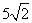 (B) 7 (C) 6 (D)
(B) 7 (C) 6 (D) 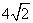
2.C[命题意图]本小题主要考查集合的概念、集合运算等集合有关知识
[解析]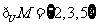 ,
,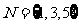 ,则
,则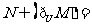
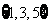
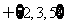 =
=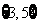
(3)若变量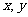 满足约束条件
满足约束条件 则
则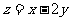 的最大值为
的最大值为
(A)4 (B)3 (C)2 (D)1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com