21．(本小题满分14分)

椭圆E的中心在原点O，焦点在x轴上，离心率，过点C(-1，0)的直线l交椭圆于A、B两点，且满足：(λ≥2)。

(1)若λ为常数，试用直线l的斜率k(k≠0)表示三角形OAB的面积；

(2)若λ为常数，当三角形OAB的面积取得最大值时，求椭圆E的方程；

(3)若λ变化，且λ=k²+1，试问：实数λ和直线l的斜率k(k∈R)分别为何值时，椭圆E的短半轴长取得最大值？并求出此时的椭圆方程。

20．(本题满分14分)

关于x的方程2x²-tx-2=0的两根为函数f(x)=

(1)求f(的值。

(2)证明：f(x)在[上是增函数。

(3)对任意正数x₁．x₂,求证：　 (文科不做)

19．(本小题满分14分)

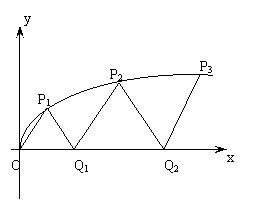(文科)如图，曲线上的点与x轴的正半轴上的点及原点构成一系列正三角形△OP₁Q₁，△Q₁P₂Q₂，…△Q_n-1P_nQ_n…设正三角形的边长为,n∈N﹡(记为),．

(1)求的值;

(2)求数列{}的通项公式;

18．(本小题满分14分)

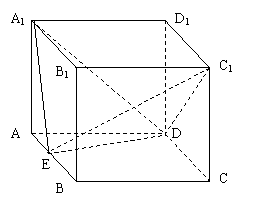
如图：直平行六面体ABCD-A₁B₁C₁D₁，底面ABCD是边长为2a的菱形，∠BAD=60⁰，E为AB中点，二面角A₁-ED-A为60⁰

(I)求证：平面A₁ED⊥平面ABB₁A₁；

(II)求二面角A₁-ED-C₁的余弦值；

(III)求点C₁到平面A₁ED的距离。

17．(本小题满分12分)

(文科)一个口袋中装有大小相同的2个白球和3个黑球．

(Ⅰ)从中摸出两个球，求两球恰好颜色不同的概率；

(Ⅱ)从中摸出一个球，放回后再摸出一个球，求两球恰好颜色不同的概率．

16．(本小题满分12分)

(文科)已知，求(1)；(2)的值．

15．已知圆C的圆心在第一象限, 与x轴相切于点, 且与直线也相切, 则该圆的方程为　　　　　　　　　　 ．

14．若，则目标函数的取值范围是　　　　　 ．

13．在的展开式中，含项的系数为____________．

12．(文科)如图是150辆汽车通过某路段时速度的频率分布直方图，则速度在 的汽车大约有　　　　　　 　辆．