
2. 设ω是正实数,如果函数 f(x)=2sinωx在[-,]上是增函数,那么ω的取值范围是
1.
函数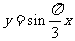 在区间
在区间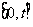 上恰好取得2个最大值,则实数t的取值范围是 .
上恰好取得2个最大值,则实数t的取值范围是 .
9. 解析:(1)
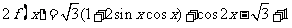
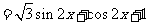
∴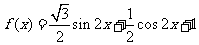
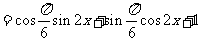
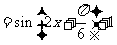
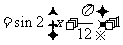
所以函数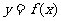 的图象可由函数
的图象可由函数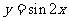 的图象向左平移
的图象向左平移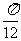 个单位,再向上平移
个单位,再向上平移
1个单位而得到
(2)∵函数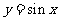 图象的对称中心为
图象的对称中心为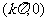 ,
,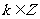 ,由
,由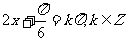
得函数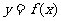 的对称中心为
的对称中心为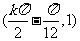 ,
, 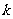 依次取1,2,3,4……可得
依次取1,2,3,4……可得
A1、A2、A3、A4……各点,
∴A4的坐标为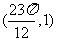
[点评](1)三角函数图像及其变换是当前考查热点,其书写的规范性是考生必须高度重视的. (2)正弦、余弦函数图象的对称中心即图象与平衡位置的交点。
三 范例剖析
例1 已知函数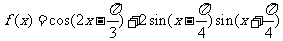
(Ⅰ)求函数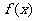 的最小正周期和图象的对称轴方程
的最小正周期和图象的对称轴方程
(Ⅱ)求函数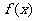 在区间
在区间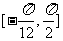 上的值域
上的值域
变题:已知函数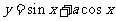 的图象关于直线
的图象关于直线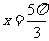 对称,则函数
对称,则函数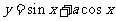 的图象在区间
的图象在区间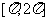 上的一条对称轴是
上的一条对称轴是
例2 已知函数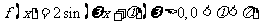 的最小正周期为
的最小正周期为 ,其图像过点
,其图像过点 .
.
(Ⅰ) 求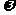 和
和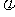 的值;(Ⅱ)
函数
的值;(Ⅱ)
函数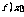 的图像可由
的图像可由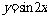 (x∈R)的图像经过怎样的变换而得到?
(x∈R)的图像经过怎样的变换而得到?
.
变题:如图,点O是做简谐运动的物体的平衡位置,取向右的
 方向为物体位移的正方向,若已知振幅为3cm,周期为3s,
方向为物体位移的正方向,若已知振幅为3cm,周期为3s,
且物体向右运动到距平衡位置最远处时开始计时.
(1)物体对平衡位置移x (cm)和时间t (s)的函数关系式:
(2)该物体在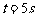 时的位置为
时的位置为
例3
在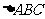 中,已知内角
中,已知内角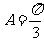 ,边
,边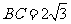 .设内角
.设内角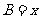 ,
,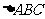 周长为
周长为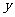 .
.
(1) 求函数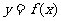 的解析式和定义域; (2)求
的解析式和定义域; (2)求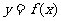 的最大值.
的最大值.
变题:设A、B、C为锐角三角形的三个内角, ,
,
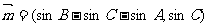 ,且满足
,且满足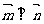 .
.
(Ⅰ)求角A的大小;(Ⅱ)求函数y=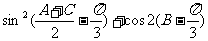 的最大值.
的最大值.
四 巩固训练
8.解析:由图象知: ,再由周期性得解为0。
,再由周期性得解为0。
7.解析:本小题主要考查三角函数图像对称性及同角三角函数关系。依题意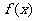 图象关于直线
图象关于直线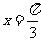 对称,所以
对称,所以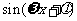 =
=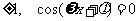 ,所以
,所以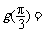
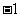
6.解析:本小题主要考查三角函数图像对称性及周期性。依题意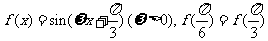 且
且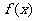 在区间
在区间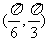 有最小值,无最大值, ∴区间
有最小值,无最大值, ∴区间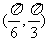 为
为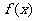 的一个半周期的子区间,且知
的一个半周期的子区间,且知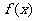 的图像关于
的图像关于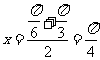 对称,∴
对称,∴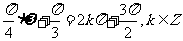 ,取
,取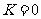 得
得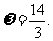 答案:
答案: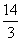
9.已知: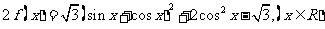
(1)请说明函数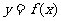 的图象可由函数
的图象可由函数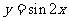 的图象经过怎样的变换得到;
的图象经过怎样的变换得到;
(2)设函数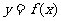 图象位于y轴右侧的对称中心从左到右依次为A1、A2、A3、A4、…、
图象位于y轴右侧的对称中心从左到右依次为A1、A2、A3、A4、…、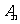 …、
…、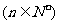 ,试求A4的坐标。
,试求A4的坐标。
二 感悟解答
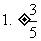 ; 2. [解析] ∵
; 2. [解析] ∵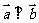 ,∴
,∴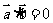 ,∴
,∴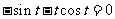 ,
, .
.
∴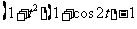 =
=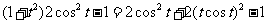
=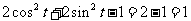
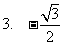 ;
;
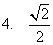 ;
;
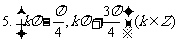
8.函数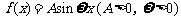 的部分图象如图所示,
的部分图象如图所示,
则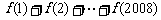 =
.
=
.
7. 若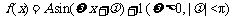 对任意实数t,都有
对任意实数t,都有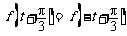 .记
.记

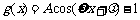 ,则
,则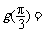
6. 已知 ,且
,且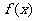 在区间
在区间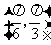 有最小值,无最大值,则
有最小值,无最大值,则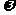 =__________.
=__________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com