
20.(本题14分)设函数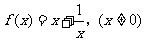 的图象为
的图象为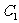 、
、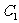 关于点A(2,1)的对称的图象为
关于点A(2,1)的对称的图象为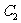 ,
,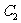 对应的函数为
对应的函数为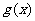 .
.
(1)求函数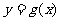 的解析式;
的解析式;
(2)若直线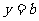 与
与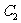 只有一个交点,求
只有一个交点,求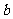 的值并求出交点的坐标.
的值并求出交点的坐标.
19.(本题14分)已知复数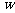 满足
满足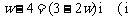 为虚数单位),
为虚数单位),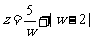 ,求一个以
,求一个以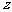 为根的实系数一元二次方程.
为根的实系数一元二次方程.
18、某农贸市场出售西红柿,当价格上涨时,供给量相应增加,而需求量相应减少,具体调查结果如下表:
表1 市场供给量
|
单价(元/kg) |
2 |
2.4 |
2.8 |
3.2 |
3.6 |
4 |
|
供给量(1000kg) |
50 |
60 |
70 |
75 |
80 |
90 |
表2 市场需求量
|
单价(元/kg) |
4 |
3.4 |
2.9 |
2.6 |
2.3 |
2 |
|
需求量(1000kg) |
50 |
60 |
65 |
70 |
75 |
80 |
根据以上提供的信息,市场供需平衡点(即供给量和需求量相等时的单价)应在区间
( )
A.(2.3,2.6)内 B.(2.4,2.6)内
C.(2.6,2.8)内 D.(2.8,2.9)内
17、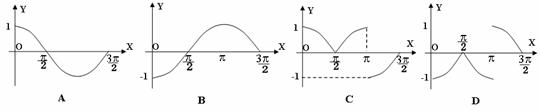
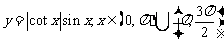 的图象是 ( )
的图象是 ( )
16、已知函数 的值域分别是集合P、Q,则 ( )
的值域分别是集合P、Q,则 ( )
A.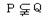 B.P=Q
B.P=Q
C.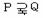 D.以上答案都不对
D.以上答案都不对
15.给出以下四个命题:①若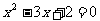 ,则
,则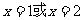 ;
;
②若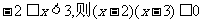 ;
;
③若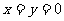 ,则
,则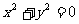 ;
;
④若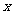 、
、
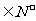 ,
,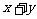 是奇数,则
是奇数,则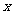 、
、 中一个是奇数,一个是偶数.则 ( )
中一个是奇数,一个是偶数.则 ( )
A.①的逆命题真 B.②的否命题真
C.③的逆否命题假 D.④的逆命题假
14.已知函数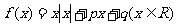 ,给出下列四个命题:①
,给出下列四个命题:①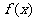 为奇函数的充要条件是q =0;②
为奇函数的充要条件是q =0;②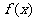 的图象关于点(0,q)对称;③当p=0时,方程
的图象关于点(0,q)对称;③当p=0时,方程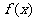 =0的解集一定非空;④方程
=0的解集一定非空;④方程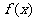 =0的解的个数一定不超过两个。
=0的解的个数一定不超过两个。
其中所有正确命题的序号是 .
13.下列命题中假命题的个数为 .
①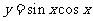 的周期为
的周期为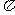 ,最大值为
,最大值为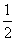 ;
;
②若x是第一象限的角,则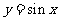 是增函数;
是增函数;
③在 中,若
中,若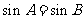 ,则
,则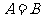 ;
;
④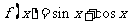 既不是奇函数,也不是偶函数;
既不是奇函数,也不是偶函数;
⑤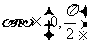 且
且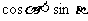 ,则,
,则, ;
;
⑥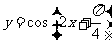 的一条对称轴为
的一条对称轴为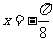
12.在高校自主招生中,某班级50人报考交大和复旦两所大学,已知每人至少报考其中一所学校。估计报考交大的人数占全班80%到90%之间,报考复旦的人数占全班32%到40%之间,设M是两所大学都报的人数的最大值,m是两所大学都报的人数的最小值,则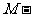 m= .
m= .
11.已知函数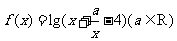 的值域为R,则实数
的值域为R,则实数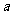 的取值范围是
.
的取值范围是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com