
7.如图在Rt ABC中,已知BC=a,若长为2a的线段PQ以A为中点,问
ABC中,已知BC=a,若长为2a的线段PQ以A为中点,问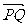 与
与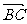 的夹角
的夹角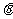 取何值时,
取何值时,
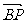
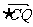 的值最大?并求出这个最大值。
的值最大?并求出这个最大值。
6. 已知O为坐标原点, 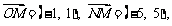 集合
集合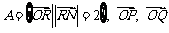
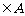
且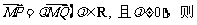
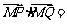 .
.
5. 设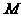 是
是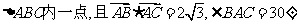
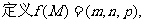 其中
其中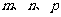 分别是
分别是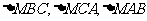 的面积,
的面积,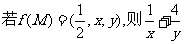 的最小值是___________.
的最小值是___________.
4.已知点O在△ABC内部,且有 ,则△OAB与△OBC的面积之比为 .(南通市2008届高三第一次调研考试)
,则△OAB与△OBC的面积之比为 .(南通市2008届高三第一次调研考试)
3. 设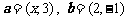 ,若
,若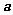 与
与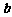 的夹角为钝角,则x的取值范围是
.
的夹角为钝角,则x的取值范围是
.
2.(08北京卷)已知向量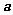 与
与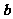 的夹角为
的夹角为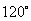 ,且
,且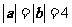 ,那么
,那么 的值为
.
的值为
.
1.(08陕西卷)关于平面向量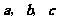 .有下列三个命题:
.有下列三个命题:
①若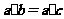 ,则
,则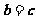 .②若
.②若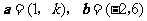 ,
,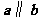 ,则
,则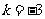 .
.
③非零向量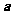 和
和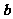 满足
满足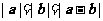 ,则
,则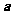 与
与 的夹角为
的夹角为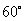 .其中真命题的序号为 .(写出所有真命题的序号)
.其中真命题的序号为 .(写出所有真命题的序号)
7.解:(I) 当 x = 时,cos <a,c> =
= …….4
= -cos x = -cos = cos
∵ 0≤<a,c>≤p, ∴ <a,c> = …………….7
(II) f (x) = 2a·b + 1 = 2 (-cos 2 x + sin x cos x) + 1 = 2 sin x cos x-(2cos 2 x-1)
= sin 2x-cos 2x = sin (2x-)
∵ x∈[,],
∴ 2x-∈[,2p], …..10
故 sin (2x-)∈[-1,]
∴ 当 2x-= ,即 x = 时,f (x)max = 1 ……14
三 范例剖析
例1 已知向量=(1+tanx,1-tanx),=(sin(x-),sin(x+)).
(1)求证:⊥; (2)若x∈[-,],求||的取值范围.(南通四县市2008届高三联合考试)
辨析:已知向量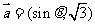 ,
,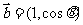 ,
,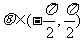 .
.
(Ⅰ)若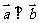 ,求
,求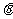 ; (Ⅱ)求
; (Ⅱ)求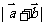 的最大值.
的最大值.
例2 在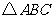 中,角
中,角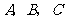 的对边分别为
的对边分别为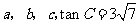 .
.
(1)求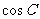 ;
;
(2)若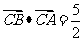 ,且
,且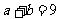 ,求
,求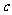 .
.
辨析:已知向量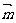 =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量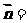 (2,0)所成角为
(2,0)所成角为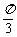 ,其中A, B, C
,其中A, B, C
是⊿ABC的内角.
(1)求角B的大小; (2)求sinA+sinC的取值范围.
例3 (2008广东六校联考)已知向量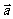 =(cos
=(cos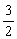 x,sin
x,sin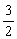 x),
x),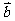 =(
=(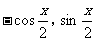 ),且x∈[0,
),且x∈[0,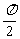 ].(1)求
].(1)求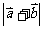 (2)设函数
(2)设函数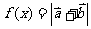 +
+ ,求函数
,求函数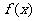 的最值及相应的
的最值及相应的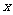 的值。
的值。
辨析:设平面向量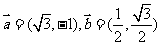 ,若存在实数
,若存在实数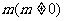 和角
和角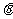 ,其中
,其中
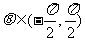 ,使向量
,使向量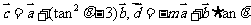 ,且
,且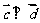 .
.
(1).求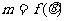 的关系式;(2).若
的关系式;(2).若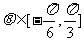 ,求
,求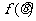 的最小值,并求出此时的
的最小值,并求出此时的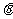 值.
值.
四 巩固训练
6.答案: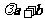 =
=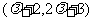 则向量
则向量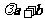 与向量
与向量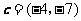 共线
共线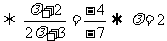
5.答案:由于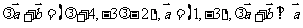
∴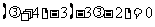 ,即
,即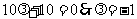 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com