
4.答案: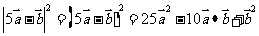 =
=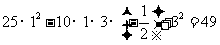 ,
, 7
7
评析:向量的模、向量的数量积的运算是经常考查的内容,难度不大,只要细心,运算不要出现错误即可
3.答案:∵ ∴
∴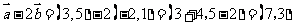
2.答案:过C作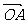 与
与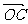 的平行线与它们的延长线相交,可得平行四边形,由角BOC=90°角AOC=30°,
的平行线与它们的延长线相交,可得平行四边形,由角BOC=90°角AOC=30°,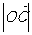 =
=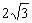 得平行四边形的边长为2和4,
得平行四边形的边长为2和4, 2+4=6
2+4=6
评析:本题考查平面向量的基本定理,向量OC用向量OA与向量OB作为基底表示出来后,求相应的系数,也考查了平行四边形法则。
1.答案:共线
7.已知向量 = (cos x,sin x), = (-cos x,cos x), = (-1,0)
(Ⅰ)若 x = ,求向量 、 的夹角;
(Ⅱ)当 x∈[,] 时,求函数 f (x) = 2· + 1 的最大值。
二 感悟解答
6.设向量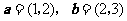 ,若向量
,若向量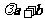 与向量
与向量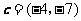 共线,则
共线,则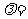 .
.
考点6:平面向量的应用
5.已知平面向量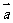 =(1,-3),
=(1,-3),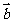 =(4,-2),
=(4,-2),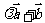 与
与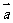 垂直,则
垂直,则 是
是
4.(2008江苏)已知向量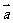 和
和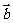 的夹角为
的夹角为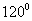 ,
,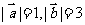 ,则
,则 .
.
考点5:平面向量的平行与垂直
3.(08四川卷文3)设平面向量 ,则
,则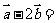
考点4:平面向量的的数量积
2.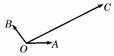 (2007陕西)如图,平面内有三个向量
(2007陕西)如图,平面内有三个向量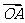 、
、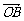 、
、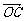 ,其中
,其中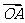 与
与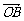 的夹角为120°,
的夹角为120°,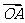 与
与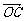 的夹角为30°,且|
的夹角为30°,且|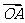 |=|
|=|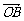 |=1,|
|=1,|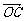 | =
| =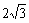 ,若
,若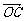 =λ
=λ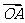 +μ
+μ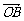 (λ,μ∈R),则λ+μ的值为
.
(λ,μ∈R),则λ+μ的值为
.
考点3:平面向量的坐标表示
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com